АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Выберем поверхность интегрирования, учитывая симметрию задачи

Читайте также:
  1. Биофизика – как наука. Практические задачи. Методы исследования
  2. Возникновение обществ содействия милиции, их правовое положение и задачи.
  3. Вычислим заряд, охватываемый этой поверхностью.
  4. Генетика, ее задачи. Наследственность и изменчивость – свойства организмов. Основные генетические понятия
  5. Задачи.
  6. Карта для внеаудиторной работы по теме № 11: Череп в целом. Топография основания черепа (наружная и внутренняя поверхность). Височная, подвисочная, крылонебная ямки.
  7. Квалифицированная медицинская помощь решает три основных задачи.
  8. Крестообразная повязка на затылок и заднюю поверхность шеи
  9. Магнитный поток через замкнутую поверхность.Вихревой характер магнитного поля.
  10. Методические указания и порядок решения задачи.
  11. Методические указания и порядок решения задачи.

Силовые линии поля - радиальные линии, поэтому поверхность интегрирования удобно выбрать в виде сферической поверхности. При таком выборе вспомогательной Гауссовой поверхности вектор напряженности электрического поля будет перпендикулярен поверхности в любой точке. Для каждой области, в которой надо найти напряженность поля, значение радиуса этой поверхности будет различное. На рисунке сечение этих поверхностей изображено штрих пунктирными линиями. Вектор внешней нормали к поверхности и вектор напряженности поля сонаправлены и угол между ними равен (α = 00) нулю.

3. Найдем поток вектора через выбранную поверхность.

По определению поток через замкнутую поверхность равен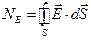

или .

В нашем случае, как это видно из рисунка, угол между векторами и всегда равен нулю градусов. Модуль вектора напряженности поля 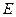из соображений симметрии имеет одинаковое значение во всех точках поверхности интегрирования и поэтому его можно вынести за знак интеграла. С учетом этого, получаем

Расстояние r от центра сфер до точки, в которой мы хотим определить напряженность поля, оно равно радиусу поверхности интегрирования. Таким образом, потоквектора для всех трех областей равен:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |

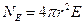
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)