Посмотрим теперь, какую форму должна в свете Теоремы 1 принимать область сходимости степенного ряда

1. Любой степенной ряд (1) сходится при .. Таким образом, точка принадлежит области сходимости любого степенного ряда. Может ли случится, что область сходимости степенного ряда состоит из единственной точки ? Ряд

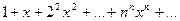
показывает, что этот случай возможен (если , то при будем иметь , и тем самым не выполнено необходимое условие сходимости числовых рядов).2.Противоположным крайним случаем является тот случай, когда ряд (1)сходится при любом , т.е. когда областью его сходимости является всячисловая прямая; что этот случай также возможен, показывает ряд

;

(при будем иметь ).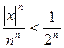

3. Во всех остальных случаях существуют такие значения , для которых ряд (1)

сходится, и такие, для которых он расходится.

Покажем, прежде всего, что область сходимости ряда (1) в этом случае есть

ограниченное множество. В самом деле, пусть – любая точка расходимости ряда (1);

в силу Теоремы 1 тогда ряд (1) должен расходится при любом , для которого и,

значит, любая его точка сходимости должна удовлетворять неравенству , что и

показывает ограниченность множества точек сходимости.

Нетрудно видеть, что если область сходимости ряда (1) не сводится к одной точке и не охватывает всю числовую прямую, то всегда существует такое , что ряд (1) сходится при 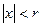и расходится при 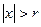. Значит для области сходимости степенного ряда (1) справедливы включения .

Условимся при рассмотрении степенного ряда считать, что при ; вся действительная прямая при . Теперь можно сформулировать полученный результат следующим образом:

Теорема 2. Для всякого степенного ряда (1) существует такое число , что ряд

абсолютно сходится при 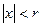и расходится при .

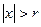Число называют радиусом сходимости.

Теорема 2раскрывает поведение степенного ряда (1) на всей числовой прямой, за исключением при .Таким образом, задача об определении сходимости степенного ряда (1) сводится к определению радиуса сходимости и исследованию поведения ряда (1) в точках при . Задача о вычислении радиуса сходимости степенного ряда (1) полностью решается теоремой Коши - Адамара. Приведе м ее частные случаи:

1) Пусть существует 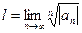. Тогда

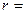
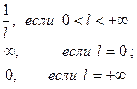
2) В том случае, когда существует он совпадает с радиусом сходимости.

Пример1 Рассмотрим ряд

.

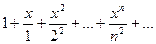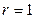Имеем ; . Таким образом . При 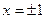ряд сходится, так как сходится гармонический ряд . Значит область сходимости этого ряда есть .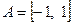

Пример 2. Рассмотрим ряд

.

Имеем 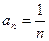; ; 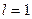; При мы получаем гармонический ряд , который, как мы знаем, расходится. При мы получаем ряд 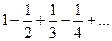, который сходится по признаку Лейбница. Значит область сходимости этого ряда есть .

Пример 3. Рассмотрим ряд

.

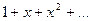Имеем ; ; 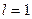. Значит область сходимости этого ряда есть .