АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Функциональные свойства суммы степенного ряда

Читайте также:
  1. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  2. Алгебраические свойства векторного произведения
  3. АЛГОРИТМ И ЕГО СВОЙСТВА
  4. Аллювиальные отложения и их свойства
  5. Анализ общей суммы затрат и з-т на 1 руб. прод-ции
  6. Анализ общей суммы затрат на производство продукции
  7. АТМОСФЕРА И ЕЕ СВОЙСТВА
  8. Атрибуты и свойства материи
  9. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
  10. Биосинтез белка и нуклеиновых кислот. Матричный характер реакций биосинтеза. Генетическая информация в клетке. Гены, генетический код и его свойства
  11. Валентные свойства атомов
  12. Валериана лекарственная - лечебные свойства, рецепты

Теорема 1. Сумма степенного ряда непрерывна в каждой точке интервала .

Теорема 2 (Абеля). Если степенной ряд (1) сходится при , то сумма

степенного ряда непрерывна в точке .

Теорема 3. Степенной ряд (1) в промежутке с концами 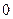и можно

интегрировать почленно:

.

Значение может совпадать и с одним из концов интервала сходимости, если на этом конце ряд (1) сходится. Радиус сходимости полученного степенного ряда совпадает с радиусом сходимости ряда (1).

Теорема 2. Степенной ряд (1) внутри промежутка сходимости можно дифференцировать

почленно, так что

.

Радиус сходимости полученного степенного ряда совпадает с радиусом сходимости ряда (1).

Замечание 1. Теорема 2 открывает возможность многократного дифференцировании

степенного ряда внутри интервала сходимости.


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)