Понятие функциональной последовательности и функционального ряда

Раздел 8: Функциональные ряды.

Рассматриваемые вопросы:

1) Понятие функциональной последовательности и функционального ряда.

2) Сходимость функциональной последовательности (функционального ряда).

3) Степенной ряд и его область сходимости.

4) Функциональные свойства суммы степенного ряда.

5) Ряд Тейлора.

6) Разложение функций в степенные ряды.

Понятие функциональной последовательности и функционального ряда.

Пусть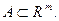

Определение 1. Сопоставим по некоторому правилу каждому натуральному числу 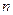функцию, заданную на множестве , и обозначим эту функцию 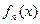. Множество занумерованных функций

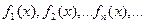(1)

Мы будем называть функциональной последовательностью и обозначать .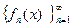

Отдельные функции 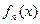мы будем называть членами или элементами рассматриваемой последовательности (1).

Множество , на котором определены все элементы последовательности, мы будем называть областью определения этой последовательности.

Определение 2. Рассмотрим функциональную последовательность 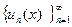, областью определения которой является множество . Символ

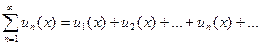(2)

мы будем называть функциональным рядом, функции 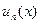-членами рассматриваемого ряда, а множество -областью определения этого ряда.

Определение 3. Сумму 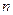первых членов ряда (2)

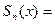
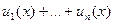
мы будем называть 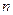-ой частичной суммой.

Отметим, что изучение функциональных рядов эквивалентно изучению функциональных последовательностей, так как каждому функциональному ряду (2) соответствует функциональная последовательность

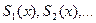(3)

его частичных сумм, и наоборот, каждой функциональной последовательности (3) соответствует функциональный ряд

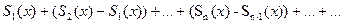, (4)

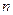-ая частичная сумма которого есть .

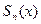Поиск по сайту: