АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Разложение функций в степенные ряды

Читайте также:
  1. Автоматизация функций в социальной работе
  2. АНАЛИЗ ФУНКЦИЙ СПЕЦИАЛИСТОВ ПО СТРАТЕГИЧЕСКОМУ МЕНЕДЖМЕНТУ И ПОЛНОМОЧИЙ ОРГАНОВ УПРАВЛЕНИЯ ОРГАНИЗАЦИИ, ПРИНИМАЮЩИХ СТРАТЕГИЧЕСКИЕ РЕШЕНИЯ.
  3. Анализ функций управления
  4. Б) Вычисление тригонометрических функций.
  5. Ввод функций вручную
  6. Взаимная ортогональность собственных функций эрмитовых операторов
  7. Взаимосвязь правопорядка и функций государства
  8. Возрастание и убывание функций. Экстремумы функции
  9. Вопрос 17 Принципы,функций и формы оплаты труда
  10. Вопрос 9 цели и функций системы управления
  11. Вопрос. Разложение аналогового сигнала в ряд Фурье.
  12. Вопрос35. Предел Функции в точке и на бесконечности. Геометрическая иллюстрация определений. Предел постоянной. Предел суммы, частного, произведения. Предел элементарных функций.

Условие бесконечной дифференцируемости функции является необходимым, но

недостаточным для разложения функции в степенной ряд. Так, например, функция

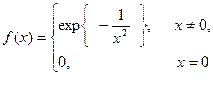
бесконечно дифференцируема на всей числовой прямой, 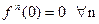, и тем самым ни

какой окрестности нуля не разлагается в степенной ряд.

Теорема1(достаточное условие разложимости функции в степенной ряд). Пусть 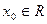, 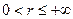. Предположим, что функция 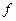удовлетворяет условиям:

1) ,

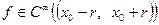2) : и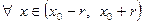

.

Тогда

.

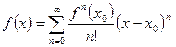Пример 1. Пусть . Тогда 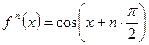, откуда .

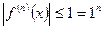Поэтому

.

Пример 2. Пусть . Тогда 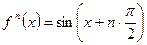, откуда .

Поэтому

.

Пример 3. Пусть . Тогда 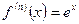. Поэтому для 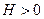будем иметь

.

Значит

.

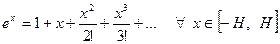Так как 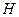было выбрано произвольно, то

.

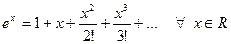Приведенная теорема дает метод разложения функций в ряд Тейлора. Однако условия

этой теоремы не всегда выполняются, или не могут быть просто проверены. Тогда эффективным методом получения разложения является использование свойств степенных рядов и их сумм.

Пример 4. Для

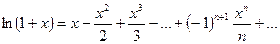
Действительно, если , то

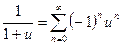(1)

Пусть фиксировано. Проинтегрируем ряд (1) почленно по промежутку с концами и . Получим

,

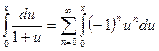поэтому

, . (2)

В силу непрерывности функции 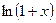имеем .

При ряд 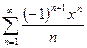, имеющий радиус сходимости , по признаку Лейбница сходится. Поэтому его сумма непрерывна в точке . Значит

.

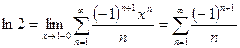Таким образом, (2) справедливо и при .

Пример 5. Для

.

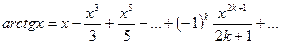Действительно, 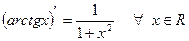. Если 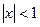, то

.

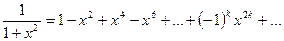На основании теоремы о почленном интегрировании степенного ряда имеем

или

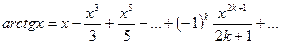
. (3)

Степенной ряд (3) по признаку Лейбница сходится и при 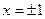. Учитывая непрерывность функции 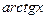заключаем, что (3) имеет место и при 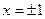. В частности

.

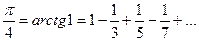Пример 6. Пусть . Тогда

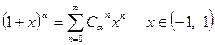, (4)

где ; , .

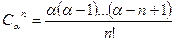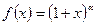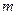Ряд называют биномиальным рядом, а его коэффициенты – биномиальными. ра для функции , . Если - натуральное число , то коэффициент при 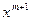и все следующие коэффициенты обратились бы в , так как их представление содержало бы множитель 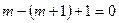, и в этом случае равенство (4) превращается в формулу бинома Ньютона.

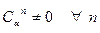Пусть .Тогда коэффициенты . Так как

,

то

. Поэтому радиус сходимости биномиального ряда равен .

Пусть , 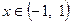. Покажем, что функция 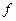удовлетворяет уравнению

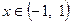. (5)

Действительно, 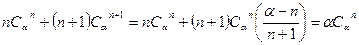, поэтому

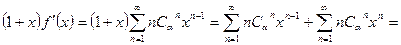
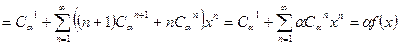. (5)

Умножим (5) на 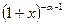. Получим

.

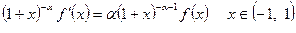Отсюда

.

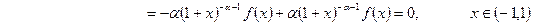Значит 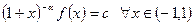. Так как , то 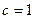, откуда , .

 


 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

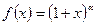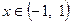Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)