Сходимость функциональной последовательности (функционального ряда)

Зафиксируем точку из области определения функциональной последовательности 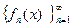(функционального ряда 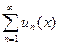) и рассмотрим числовую последовательность 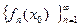(числовой ряд ). Если указанная числовая последовательность (числовой ряд) сходится, то говорят, что функциональная последовательность (функциональный ряд) сходится в точке .

Множество всех точек, в которых сходится данная функциональная последовательность (функциональный ряд), называется областью сходимости этой последовательности (ряда).

В конкретных случаях область сходимости может совпадать с областью определения, являться подмножеством области определения или вообще быть пустым множеством.

Предположим, что функциональная последовательность 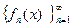имеет в качестве области сходимости некоторое множество .

Определение 1. Функция 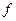, заданная на множестве равенством

,

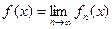называется предельной функцией последовательности .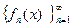

Определение 2. Если функциональный ряд 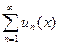имеет в качестве области сходимости некоторое множество , то на этом множестве определена функция , являющаяся предельной функцией последовательности частичных сумм этого ряда и называемая его суммой.

Поиск по сайту: