АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Степенной ряд и его область сходимости

Читайте также:
  1. Алгоритм наложения согревающего компресса на околоушную область
  2. Амурская область
  3. Аналіз бюджетного фінансування соціального захисту населення в регіоні (Калуський район, Івано-Франківська область)
  4. Виды статистических величин, их применение в медицине. Интенсивные коэффициенты и коэффициенты соотношения, методика расчета, область применения.
  5. Глазная область
  6. Для целей диагностирования область возможных значений измеряемого параметра часто разбивается на интервалы и характерным является наличие параметра в данном интервале.
  7. Закон кулона и область его применения.
  8. Информатизация образования как процесс и область педагогического знания
  9. Коаксиальный кабель: устройство, классификация по европейским и американским стандартам, область применения и тенденции.
  10. Количество зарегистрированных преступлений и других правонарушений, Пензенская область на 100 тыс. среднегодовое число
  11. Компоненты и область действия
  12. Критерий Коши сходимости несобственного интеграла первого рода. Достаточные признаки сходимости.

Определение 1.Степенным рядом на зывается функциональный ряд вида

, (1)

или более общо

,

где 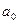, , … , … 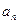- постоянные вещественные числа.

Степенные ряды наиболее просты в теоретическом отношении и наиболее важны для большинства приложений.

Как и для всякого функционального ряда, мы должны при изучении ряда (1) в первую очередь поставить вопрос о его области сходимости. Форма области сходимости степенного ряда является следствием следующего важнейшего свойства рядов этого класса.

Теорема 1. Если ряд (1) сходится при , то он абсолютно сходится при

любом значении , для которого .
Геометрическая иллюстрация: если степенной ряд сходится в некоторой точке числовой прямой, то в любой точке, более близкой, чем , к точке 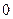, он будет сходится абсолютно.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)