Для целей диагностирования область возможных значений измеряемого параметра часто разбивается на интервалы и характерным является наличие параметра в данном интервале

Сложным признаком (разряда m) называется результат наблюдения (обследования), который может быть выражен одним из m символов. Если, как обычно, в качестве символов выбрать цифры, то сложный признак (разряда m) может быть выражен m – разрядным числом (сложный признак 8-го разряда выражается восьмеричным числом). Сложный признак может быть связан и с обследованием качественного характера, если оценка содержит несколько градаций. Разряды признака называются диагностическим интервалом.

Одноразрядный признак (m=1) имеет только одно возможное состояние. Такой признак не несет какой-либо диагностической информации и его следует исключить из рассмотрения.

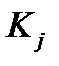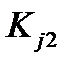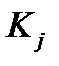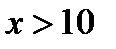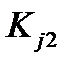Двухразрядный признак (m=2) обладает двумя возможными состояниями. Состояния двухразрядного признака можно обозначить и . Так например, признак относится к измерению параметра x, для которого установлено два диагностических интервала: и . Тогда соответствует , а обозначает 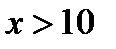. Эти состояния альтернативны, так как реализуется только одно из них. Очевидно, что двухразрядный признак может быть заменен простым признаком 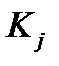, если считать и .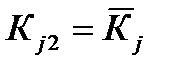

Трехразрядный признак (m=3) имеет три возможных значения: , , 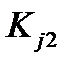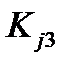. Пусть, например, для параметра x приняты три диагностических интервала: 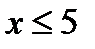, , 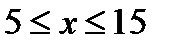. Тогда для признака 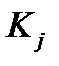, характеризующего этот параметр, возможны три значения: (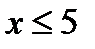); 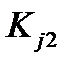(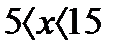); 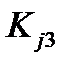(), где m-разрядный признак 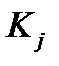имеет m возможных состояний: , ,… .

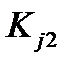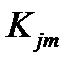Если в результате обследования выявлено, что признак 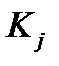имеет для данного объекта значение , то это значение будем называть реализацией признака 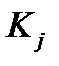. Обозначая ее 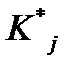, будем иметь .

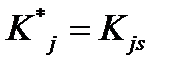В качестве диагностического веса Z реализации признака 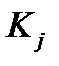для диагноза 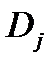может быть принято:

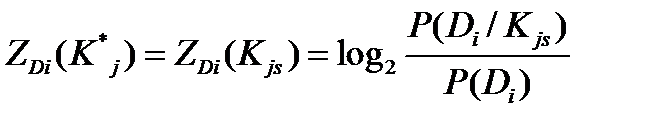(21)

где 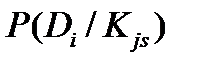- вероятность диагноза D при условии, что признак 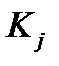получил значение , - априорная вероятность диагноза.

Если вероятность состояния D после того, как стало известно, что признак 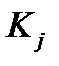имеет реализацию в интервале S, увеличилась 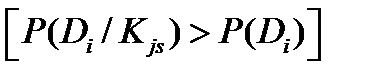, то 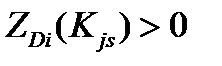, т.е. диагностический вес данного интервала признака для данного диагноза положителен. Если наличие параметра в интервале S не изменяет вероятности диагноза, то , так как .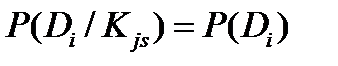

Диагностический вес на интервале S признака 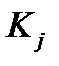по отношению к диагнозу 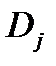, может быть отрицательным (отрицание диагноза).

Диагностический вес наличия признака 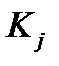в интервале S можно представить в виде, более удобном для конкретных вычислений:

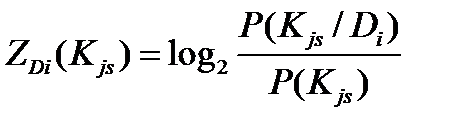(22)

где 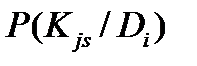- вероятность появления на интервале S признака 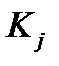для объектов с диагнозом , 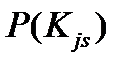- вероятность появления этого интервала у всех объектов с различными диагнозами.

Эквивалентность равенств (21) и (22) следует из следующего тождества:

.

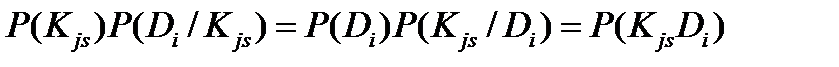Равенства (21), (22) определяют независимый диагностический вес данной реализации признака для диагноза . Он характерен для ситуации, в которой обследование по признаку 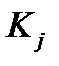проводится первым или когда результаты обследования по другим признакам еще неизвестны (например, при одновременном обследовании по нескольким признакам). Он также характерен для случая, когда вероятность появления данной реализации признака не зависит от результатов предыдущих обследований.

Однако известно, что диагностическое значение реализации признака во многих случаях зависит от того, какие реализации признаков получились в предыдущих обследованиях. Бывает, что сам по себе признак не имеет существенного значения, но его появление после некоторого другого позволяет однозначно поставить диагноз (установить состояние системы).

Пусть проводится обследование сначала по признаку 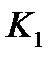, а затем по признаку 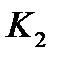. При обследовании объекта по признаку 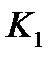была получена реализация 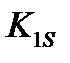, и требуется определить диагностический вес реализации признака 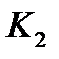для диагноза .

В соответствии с определением диагностического веса:

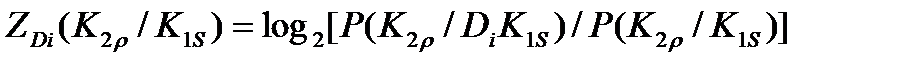(23)

Выражение (23) определяет условный диагностический вес реализации признака. Независимый диагностический вес этой реализации:

.

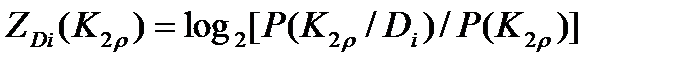Если признак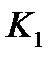и и 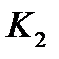являются независимыми для всей совокупности объектов с различными диагнозами (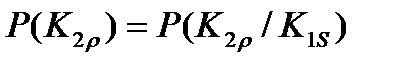) и условно независимыми для объектов с диагнозом (), то условный и независимый диагностические веса реализации совпадают.

Диагностический вес той или иной реализации признака еще не дает представления о диагностической ценности обследования по данному признаку. Например, при обследовании по простому признаку может оказаться, что его наличие не имеет диагностического веса, тогда как его отсутствие чрезвычайно важно для установления диагноза.

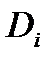Установим, что диагностическая ценность обследования по признаку для диагноза есть величина информации, вносимая всеми реализациями признака в установление диагноза .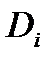

Для m – разрядного признака:

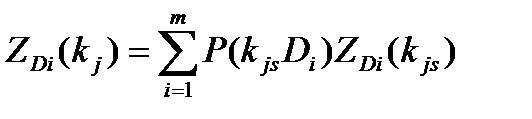
Диагностическая ценность обследования учитывает все возможные реализации признака и представляет собой математическое ожидание величины информации, вносимой отдельными реализациями. Так как величина 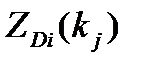относится только к одному диагнозу 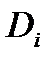, то это частная диагностическая ценность обследования по признаку _, и она определяет независимую диагностическую ценность обследования. Значение 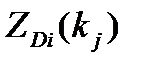характерно для случая, когда обследование производится первым или когда результаты других обследований неизвестны.

Наибольшую диагностическую ценность имеют обследования по признакам, которые часто встречаются при данном диагнозе, а вообще редко и, наоборот, по признакам, встречающимся при данном диагнозе редко, а вообще – часто. При совпадении 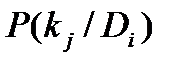и обследование не имеет никакой диагностической ценности.

Диагностическая ценность обследования вычисляется в единицах информации (двоичных единицах или битах) и не может быть отрицательной величиной. Это понятно из логических соображений: информация, полученная при обследовании, не может «ухудшить» процесс распознавания действительного состояния.

Величина 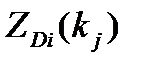может быть использована не только для оценки эффективности обследования, но и для целесообразного выбора величины диагностических интервалов (числа разрядов). Очевидно, что для упрощения анализа удобно уменьшать число диагностических интервалов, однако это может привести к уменьшению диагностической ценности обследования. С увеличением числа диагностических интервалов диагностическая ценность признака возрастает или остается прежней, но анализ результатов становится более трудоемким.

Поиск по сайту: