АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Измерение информации

Читайте также:
  1. III. ИЗМЕРЕНИЕ ИНФОРМАЦИИ
  2. YIII.3.3.Измерение
  3. АЛГОРИТМ СБОРА ИНФОРМАЦИИ
  4. Анализ отечественного рынка средств защиты информации
  5. Архивация информации
  6. Атрибуты невербальной информации
  7. Базы данных как важнейший источник социологической информации
  8. Безработица: сущность, типы. Измерение уровня безработицы. Экономические и социальные последствия.
  9. Библиографическое описание как форма свертывания информации
  10. Блок приема, переработки и хранения информации
  11. В. Измерение неравенства доходов
  12. Валовый внутренний продукт и его измерение по доходам и расходам.

Количество информации – есть разность неопределенностей (энтропий) системы до и после получения информации.

Если начальная энтропия системы равна H(A), а после получения информации она составляет H*(A), то внесенная информация .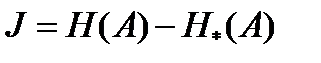

Зачастую информация относительно системы А получается с помощью наблюдения за другой, связанной с ней системой В. Обычно эта вторая система (система сигналов) дает информацию о состоянии основной системы. Среднюю величину этой информации, или информативность системы В относительно системы А, можно определить из равенства

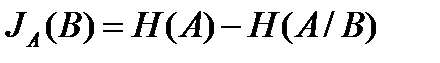(9)

В правой части соотношения (9) содержится разность первоначальной энтропии системы А и ее энтропии после того, как стало известным состояние системы сигналов В. Так как системы сигналов А и В являются связанными, то, в свою очередь, знание состояния системы А изменит априорную вероятность состояний системы В.

Средняя информация, содержащаяся в системе А относительно системы В:

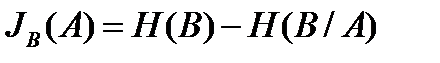(10)

Установлено, что для сложной системы, объединяющей две статистически зависимые системы, верно равенство .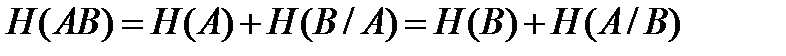

В силу этого соотношения, для информации будет верно выражение:

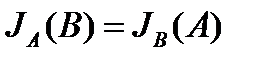(11)

Равенство (11) выражает важное свойство взаимности информации. В окончательном виде выражение для информации, которую несет система сигналов В относительно состояния системы А будет иметь вид:

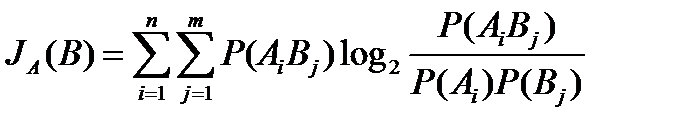(12)

 

Если системы А и В независимы, то 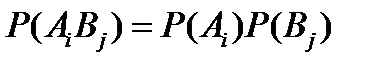и тогда из выражения (12) вытекает:

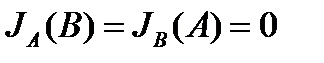
С физической точки зрения результат очевиден – наблюдение над одной из систем не может дать информации относительно другой, если между состояниями этих систем нет связи.

Величина 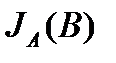представляет собой ожидаемое значение информации, содержащейся в системе В относительно всех состояний системы А. Если 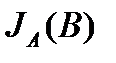– средняя информация, содержащаяся в системе В относительно состояния Аi, то естественно считать, что:

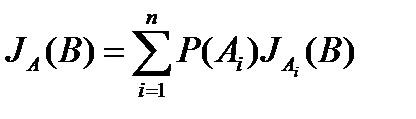(15)

Объединив выражения (13) и (15), можно записать:

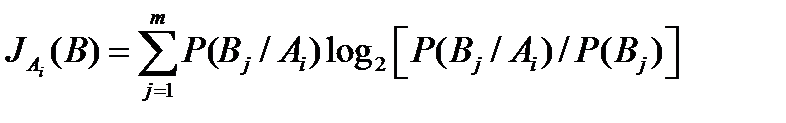(16)

Это выражение в эквивалентной форме будет иметь вид:

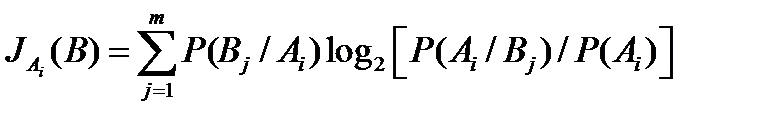(17)

Более удобным для вычислений является выражение вида:

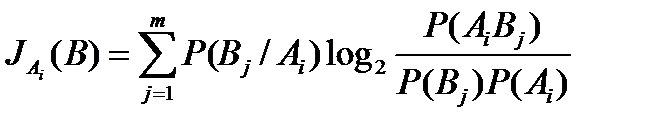
Так как системы А и В статистически зависимые, то знание состояний системы А дает информацию относительно системы В. Соответственно можно записать:

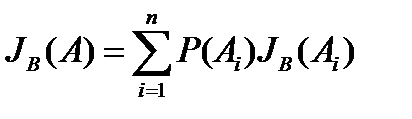
где 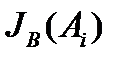- информация, которой обладает состояние Аi относительно системы В.

По аналогии следует 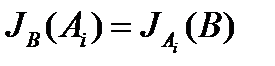. Легко проследить и другие подобные зависимости, вытекающие из свойства зависимости информации.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)