АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Обозначение H(A) показывает, что энтропия относится к системе А

Читайте также:
  1. A) к любой экономической системе
  2. HMI/SCADA – создание графического интерфейса в SCADА-системе Trace Mode 6 (часть 1).
  3. Административное право, как отрасль права в системе Российского права.
  4. Анализ прибыли по системе «директ-костинг»
  5. АСПЕКТЫ ПРОБЛЕМ В СИСТЕМЕ ОТНОШЕНИЙ ОБЩЕСТВО - ПРИРОДА
  6. Афферентный – понятие, характеризующее ход процесса нервного возбуждения по нервной системе в направлении от периферии тела к головному мозгу.
  7. Билет 10. Петр I. Характеристика внутренней политики. Экономическое развитие, социальные перемены, изменения в политической системе.
  8. Болезнь относится к предраковым состояниям.
  9. Братья Карамазовы» в системе романов Ф.М.Достоевского.
  10. Бухгалтерский и налоговый учет в системе налога
  11. В движущейся системе отсчета время течет медленнее.
  12. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Так как вероятности состояний системы 0≤Р(Аi)≤1, то энтропия представляет существенно положительную величину.

Исходя из соблюдения физической наглядности, целесообразно вычисление энтропии системы с помощью двоичных логарифмов, тогда:

(3)

Целесообразность использования двоичных (3) логарифмов легко оценить, вычисляя энтропию системы, имеющей два равновероятных состояния. В этом случае Р(А1)= Р(А2)=0,5, по выражению (3) находим:

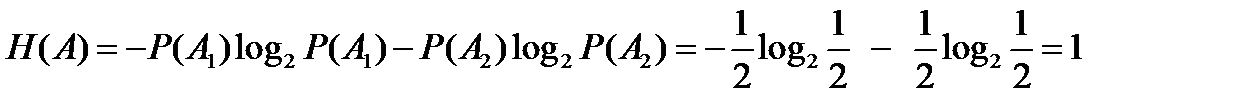
Может быть введено понятие «неопределенности» отдельного состояния системы:

(4)

Энтропия системы представляет собой среднее значение энтропий отдельных состояний:

(5)

.

Оно представляет энтропию как математическое ожидание случайной величины .

 

 

Энтропия обладает определенными свойствами:

1. Если система А имеет одно из возможных состояний Аi с вероятностью Р(Аi)=1, то энтропия такой системы ,т.к. в системе нет никакой неопределенности.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)