При изучении технических объектов, в том числе в целях их диагностирования, приняты два подхода: функциональный и структурный

Функциональный подход заключается в рассмотрении только алгоритмов функционирования объекта (реализуемых объектом функций).

Структурный подход предусматривает исследование не только реализуемых функций, но также внутренней организации или структуры объекта.

При функциональном подходе исследуемый объект рассматривают как «черный ящик», внутреннее устройство которого либо неизвестно, либо не имеет значения.

Зачастую входные и внутренние координаты объекта называют входными и соответственно внутренними переменными, а выходные координаты – выходными функциями. Входные переменные и выходные функции могут быть сопоставлены соответственно, как основным (необходимым в условиях применения объекта по назначению), так и дополнительным (предусмотренным для целей диагностирования) входами- выходам объекта.

Пусть Х есть n – мерный вектор, компонентами которого являются значения n входных переменных , а Z есть К -мерный вектор значений К-выходных функций , объекта. Согласно определению дискретного объекта число возможных значений входных переменных, как и выходных функций, конечно. Тем самым число возможных различных значений векторов X и Z также конечно и в двоичном случае не превышает и соответственно .

Под записью понимается зависимость, реализуемых исправным дискретным комбинационным объектом выходных функций Z от его входных переменных X. Зависимость (1) является математической моделью исправного дискретного комбинационного объекта и в том или ином конкретном случае может быть представлена в табличной, аналитической, графической или какой – либо другой форме.

Комбинацию значений входных переменных комбинационного дискретного объекта с n входами, называемую «входным набором» обозначим . При фиксированном порядке двоичных входных переменных каждый входной набор может быть представлен n -разрядным двоичным числом.

Комбинацию значений выходной функции комбинационного объекта с к выходами называют «выходным набором» и обозначают символом ., если данный выходной набор получен при подаче на объект входного набора . Выходные наборы также могут быть представлены (к - разрядными) двоичными числами.

Выходные функции являются булевыми функциями двоичных входных переменных , для задания которых используют таблицу истинности. Столбцам таблиц истинности соответствуют входные переменные (в левой части) и выходные функции (в правой части). В строке j –таблицы истинности обычно в виде двоичных чисел записываются входной набор и соответствующий ему выходной набор . Таблица 2 является таблицей истинности, задающей две булевы функции и от трех входных переменных

Табл.2.

Номер строки	Входные наборы	Выходные наборы

В первом слева столбце этой таблицы указаны номера строк, являющиеся в данном случае десятичными эквивалентами двоичных чисел, представляющих входные наборы.

От таблицы истинности, являющейся табличной формой функциональной математической модели комбинационного объекта, можно перейти к его аналитической функциональной модели, представляя выходные функции, например, в виде формул булевой алгебры.

В рамках функционального подхода для более или менее сложных объектов нельзя достичь требуемых значений таких показателей диагностирования, как глубина поиска и полнота обнаружения дефектов. Этим объясняется необходимость применения структурных математических моделей объекта диагностирования вообще и комбинационных дискретных объектов в частности.

Дискретные объекты состоят, как правило, из отдельных компонент, соединенных между собой определенным образом с целью получения требуемых функциональных зависимостей. Часто компонента объекта- это конструктивно и функционально законченная элементарная часть объекта, не подлежащая дальнейшему расщеплению. Поэтому для описания компоненты достаточно ее функциональной математической модели. Комбинационные дискретные объекты состоят из комбинационных компонент, называемых логическими элементами.

В качестве структурной логической модели исправного комбинационного дискретного объекта обычно принимают правильную логическую сеть (схему). Множество функционально разных логических элементов объекта называют базисом логической сети, и обозначают символом Н. Логическая сеть определяется множествами: логических элементов из базиса Н, входных полюсов и выходных полюсов. Каждому входному (выходному) полюсу взаимно однозначно соответствует входная переменная , (выходная функция ).

Логической сети соответствует ориентированный граф вершинам которого соответствуют логические элементы, входные и выходные полюсы сети, а направленным дугам – соединения сети. На рис 4 изображена логическая сеть комбинационного дискретного объекта в булевом базисе. В сети имеется четыре входа и один выход Z.

Рисунок 4 – Логическая сеть

При строго детерминированной постановке задач диагностирования всегда предполагается, что обнаружению или поиску подлежит конечное множество возможных физических дефектов объекта. В дальнейшем, наряду с термином «дефект» используется и термин «неисправность», под которой понимается формализованная (математическая) модель физического дефекта. Различают одиночные и кратные неисправности. Под одиночной понимается неисправность, принимаемая в качестве элементарной, т.е. такая, которая не может быть представлена совокупностью других, более «мелких» неисправностей. Кратная неисправность, является совокупностью одновременно существующих двух и более одиночных неисправностей.

Под физической неисправностью (дефектом) дискретного объекта понимают последствия некоторого события (явления), которое преобразует исправный объект А в некоторый другой, неисправный объект и поддерживает его в этом i - неисправном состоянии в течении интервала времени (входы объекта А однозначно соответствуют входам объекта ).

Одни и те же последствия некоторого события в разных случаях могут классифицироваться либо как неисправность объекта, либо как исправность. Это зависит от условий определяющих конкретную постановку задачи диагностирования, и находит формальное отражение в выборе математических моделей объекта диагностирования и его неисправностей. Например, возможны последствия, которые являются неисправностями при описании объекта на структурном уровне и не являются таковыми при функциональном описании объекта.

Вне зависимости от того, какая модель используется при описании исправного объекта А, множество всех неисправностей которые могут в нем возникнуть, условно делят на два класса. Неисправность называют правильной, если i-неисправный объект описывается моделью, принятой для описания исправного объекта. В противном случае неисправность называют неправильной.

Исследуемый объект 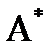считают содержащим неисправность , т.е. , если при сравнении со своим исправным эталоном А в нем найдется по крайней мере один входной набор , на котором выходной набор исправного объекта отличен от выходного набора исследуемого объекта.

Наиболее общий характер имеет модель объекта диагностирования в виде таблицы функций неисправности (ТФН), представляющая результаты работы (проверки) объекта в работоспособном и не работоспособном состояниях (таблица 3).

Таблица 3

Проверка	Результат R проверки для системы, находящейся в состоянии

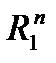
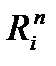
Эта таблица является явной моделью и может быть построена для объекта любой физической природы. В строках таблицы указываются все возможные проверки , которые могут быть использованы в процедуре диагностирования, и следовательно, включены в тест. Столбцы таблицы соответствуют исправному и всем возможным неисправным состояниям , ,… . Каждое неисправное состояние соответствует одной неисправности (одиночной или кратной) из заданного класса неисправностей, относительно которого строится тест. Физический смысл состояний и проверок определяется конкретными особенностями объекта диагностирования. На пересечении i-го столбца, и j-ой строки проставляется результат j-ой проверки для системы, находящейся в i-ом состоянии. Если значение проверки в объекте с j-ой неисправностью совпадает с ее значением в исправном объекте, то в таблице записывается значение =1, в противном случае записывается значение =0. Таким образом, информация в таблицу функций неисправности записывается в двоичном коде.

В таблице 4 приведен конкретный пример таблицу функций неисправности. Столбец всегда заполняется одними единицами. Если две графы заполнены одинаково, то они соответствуют эквивалентным неисправностям и могут быть объединены. В табл. 4 такими являются столбцы и . Если во всех элементах столбца проставлены единицы (столбец ), то он соответствует неисправности, которая не может быть обнаружена принятым методом диагностирования. Такой столбец исключается из ТНФ. На основании указанных свойств строится преобразованная ТФН (таблица 5), из которой также исключается столбец . ТФН содержит всю необходимую информацию для получения тестов, которые находят с помощью специальной математической обработки таблицы.

Поиск по сайту: