Алгоритм Гаусса вычисления ранга матрицы

1. Если все элементы a_ij равны нулю, то rangA=0.

2. В противном случае приводим первую строку к виду 1 0 0 0 … 0 по следующей схеме:

1) Выбираем отличный от нуля элемент матрицы (для примера пусть а₂₃≠0)

2) Помещаем этот элемент в левый верхний угол (меняя местами строки 2-ую и 1-ую и столбцы 3-й и 1-ый)

3) Комбинируя первую строку с другой, умноженную на некоторое число, с тем, чтобы новый элемент а₁₁=1

4) Соответствующими комбинациями обращаем все остальные элементы первой строки в нули

5) Если в заштрихованной части матрицы все элементы равны нулю, то ранг матрицы равен 1.

3. Если хотя бы один элемент отличен от нуля, то пункт 2 повторяется только в качестве разрешающего элемента будет а₂₂. . Если в заштрихованной области все элементы равны нулю, то ранг матрицы будет равен 2.

4. Окончательно получим 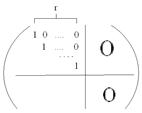. Следовательно rangA=r.

Пример. Определить ранг и базисный минор матрицы:

В первом преобразовании поделили 1-ую, 3-ю и 4-ую строки на 2; затем поменяли местами 1-ый и 2-ой столбцы, далее вычли из третьего столбца первый и наконец умножили второй столбец на 2 и вычли из третьего. В результате всех преобразований получили, что rangA=2.

Замаркировав базисные строки и столбцы и пройдя в обратном порядке, получим базисный минор

6. Матричный методы решения система линейных уравнений. Теорема Кронекера-Капелли

Определение Системой m линейных уравнений с n переменными называется система вида

,

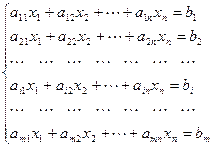где a_ij, b_i, , - произвольные числа, называемые, соответственно, коэффициентами при переменных и свободными членами уравнений.

Определение Решениемсистемы (1) называется такая совокупность чисел k_i, при подстановке которых в систему вместо переменных x_i, каждое уравнение системы обращается в верное равенство.

Определение Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Определение Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более одного решения.

Определение Две системы называются равносильными, если они имеют одно и то же множество решений.

Запишем систему (1) в матричной форме.

Пусть где A – матрица коэффициентов при переменных (она называется матрицейсистемы), X – вектор–столбец переменных, B - вектор–столбец cсвободных членов.

Так как число столбцов матрицы A равно числу строк вектор–столбца X, то их произведение 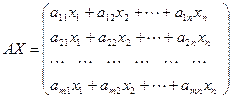есть вектор–столбец. Его элементами являются левые части системы (1).

На основании определения равенства матриц систему (1) можно записать в так называемом матричном виде: AX = B. (2)

Определение Матричным уравнением называется уравнение, в котором роль неизвестной играет некоторая матрица Х.

Простейшими примерами таких уравнений могут служить уравнения AX=C; XB=C; AXB=C, где Х и С- прямоугольные матрицы равных размеров, А и В- квадратные матрицы соответствующих размеров. Если предположить, что 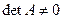и , то эти уравнения имеют единственные решения.

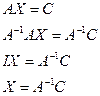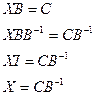1) 2) 3)

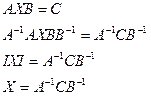
Определение. Матрица системы, дополненная справа столбцом свободных членов, называется расширеннойматрицейсистемы:

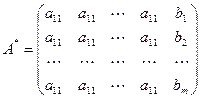
ТеоремаКронекера – Капелли (необходимое и достаточное условие совместности системы линейных уравнений). Для того, чтобы система (1) была совместной, необходимо и достаточно, чтобы ранг матрицы A системы был равен рангу расширенной матрицы A^*.

Пример. Исследовать систему линейных уравнений на совместность:

.

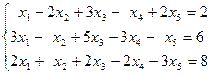Решение. Составим основную матрицу системы 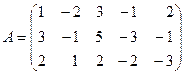и найдем ее ранг:

Составим расширенную матрицу системы и найдем ее ранг:

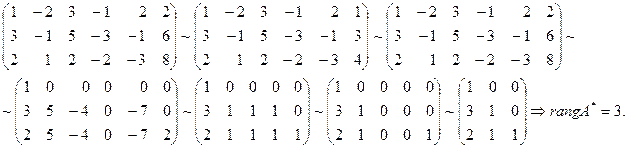
rangA¹ rangA^* Þ по теореме Кронекера–Капелли система линейных уравнений несовместна.

7. Решение системы линейных уравнений методом обратной матрицы.

Пусть m=n. Тогда мы можем вычислить определитель системы det A. Предположим, что detA¹0. В этом случае выражение (2) можно рассматривать как матричное уравнение AX=B, которое имеет единственное решение X=A^-1B, которое и будет решением СЛУ.

Пример. Решить систему линейных уравнений: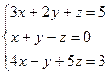

Решение.

; det A = 15-1-8-4-3-10 = -11 ≠ 0 Þ A^-1 существует.

Вычислим алгебраические дополнения элементов матрицы:

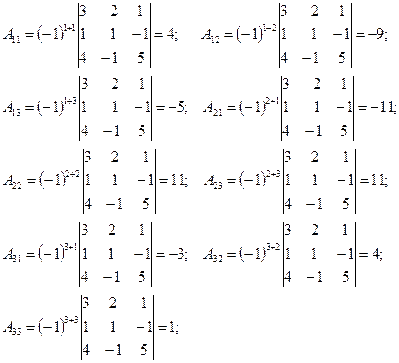
Обратная матрица равна .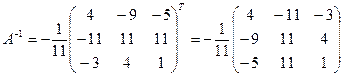

Вектор-столбец неизвестных переменных равен произведению обратной матрицы и вектора-столбца свободных членов:

Следовательно, решением данной системы линейных уравнений будут числа: x=-1; y=3; z=2.

8. Решение системы линейных уравнений методом Крамера.

Теорема Крамера. Пусть D=detA, а D_j - определитель матрицы, полученной из A заменой j -го столбца столбцом свободных членов. Тогда, если D¹0, то СЛУ имеет единственное решение, определяемое по формулам: xj = 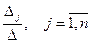(3)

Если D=0, а хотя бы один из определителей D₁, D₂,....., D_n ¹0, то система несовместна.

Если D=D₁=D₂ =... =D_n=0, то система имеет бесконечное множество решений.

Формулы (3) называются формулами Крамера.

Решим предыдущий пример по формулам Крамера.

D= -11; D₁ =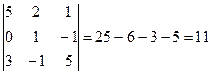

D₂ = = 3-20+9-25 = -33

D ₃ = 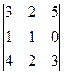= 9-5-20-6 = -22

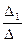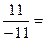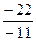x = = -1; y = =3; z = =2.

9. Решение системы линейных уравнений методом Гаусса.

Сущность метода Гаусса состоит в том, что посредством элементарных преобразований расширенная матрица системы (1) приводится к диагональному или ступенчатому виду, из которого все решения системы усматриваются непосредственно. Метод Гаусса состоит из прямого хода и обратного.

Прямой ходметодаГаусса.

Пусть в системе (1) коэффициент a₁₁¹0. Если бы было a₁₁=0, то на 1-ое место в системе (1) мы поставили бы уравнение, в котором коэффициент при x₁ отличен от нуля. Элемент а₁₁ называется разрешающимэлементом на 1-ом шаге, строка и столбец, в которых он находится - разрешающимистрокойистолбцом.

Шаг 1 (исключение переменной x₁ из всех уравнений системы, кроме 1-го). Элементы 1^ой строки остаются неизменными. Элементы 1-го столбца, расположенные ниже элемента а₁₁, обращаются в нули и остаются таковыми до конца преобразований. Все прочие элементы матрицы вычисляются по правилупрямоугольника: преобразованный элемент равен разности произведений элементов главной и побочной диагоналей.

...........

... a_ks... a_kj... a_ij = a_ksa_ij - a_kja_is

........... a_ks - разрешающий элемент

... a_is... a_ij... a_ij - пересчитываемый элемент

В результате преобразований получим матрицу:

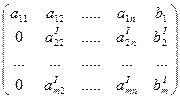
Шаг 2. Если в этой матрице встречается строка (0 0... 0 ), где ¹0, то система (1) несовместна. Если этого не произойдет, то, предполагая, что 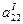¹0, изо всех строк, кроме первых двух, исключим, аналогично шагу 1, неизвестную x₂.

Аналогичная процедура проводится для исключения остальных неизвестных. При этом все элементы разрешающей строки и строк, расположенных выше, остаются неизменными; элементы разрешающего столбца, расположенные ниже разрешающего элемента, обращаются в нули и остаются таковыми до конца преобразований, все прочие элементы вычисляются по правилу прямоугольника (разрешающими элементами являются диагональные элементы матрицы).

Обратный ход метода Гаусса.

Для обнуления верхнего треугольника матрицы (выше главной диагонали) используется обратныйход. Если при прямом ходе разрешающими последовательно выбирались элементы главной диагонали матрицы, то при обратном ходе таковыми будут элементы той же диагонали, но выбираемые в обратном порядке. Пересчет элементов матрицы при обратном ходе выполняется по следующим правилам:

1) элементы разрешающей строки остаются неизменными;

2) элементы разрешающего столбца, расположенные выше разрешающего элемента, обращаются в нули и остаются таковыми до конца преобразований;

3) все прочие элементы вычисляются по правилу прямоугольника.

Если к расширенной матрице справа приписать столбец S, составленный из сумм элементов соответствующих строк, и преобразовывать его по правилам гауссовых исключений, то после каждого шага сумма элементов i-ой строки расширенной матрицы должна равняться соответствующему элементу преобразованного столбца S. Контроль вычислений можно осуществлять как при прямом, так и при обратном ходе.

Замечание. Правило прямоугольника соответствует следующим элементарным преобразованиям: умножению пересчитываемой строки на разрешающий элемент и вычитанию из полученной таким образом строки разрешающей строки, умноженной на элемент, находящийся в пересчитываемой строке в разрешающем столбце.

ДостоинстваметодаГаусса.

1) Значительно менее трудоёмкий по сравнению с другими методами.

2) Позволяет однозначно установить, совместна система или нет, а в случае совместности найти её решения (единственное или бесконечное множество).

3) Даёт возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.

НедостаткиметодаГаусса.

1) Если ведущий элемент равен нулю, то схема непригодна.

2) Данная схема чувствительна к ошибкам округления – большие погрешности при делении на малые числа, появление больших по величине промежуточных результатов, потеря точности при вычитании больших (близких друг к другу) чисел.

Пример. Решим методом Гаусса ту же самую СЛУ, которую мы решали методами обратной матрицы и методом Крамера.

~ =

= ~ ~

~ =

= ~

~ = = ~

~ =

= ~

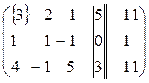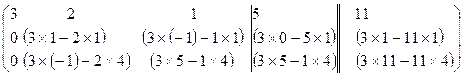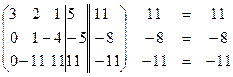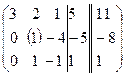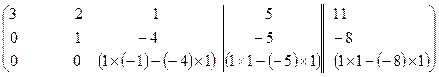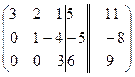
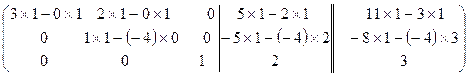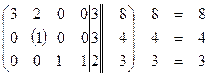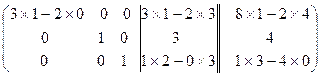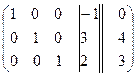
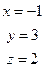
ВычислениеопределителяметодомГаусса.

Прямым ходом метода Гаусса определитель приводится к диагональному виду с той же лишь разницей, что на каждом шаге определитель делится на разрешающий элемент с показателем степени, равным количеству преобразуемых строк; при перестановке строк определитель меняет знак на противоположный; общий множитель строки (столбца) выносится за знак определителя.

Пример. Вычислить определитель: .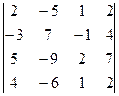

Решение.

=

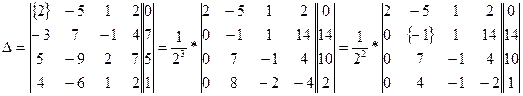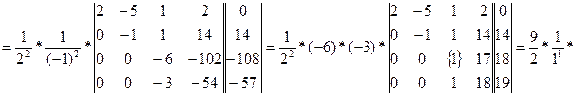
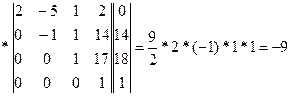(т.к. определитель треугольной матрицы равен произведению элементов главной диагонали).

СхемаметодаГауссасвыборомглавногоэлементапостолбцамматрицы.

Перед исключением x₁ отыскивается 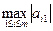. Этот элемент называется главнымэлементом. Допустим, максимум соответствует i=i₀.Тогда 1-ое уравнение в исходной системе линейных уравнений меняем местами с i₀–ым уравнением. После этого осуществляется 1-ый шаг исключения. Затем перед исключением x₂ из оставшихся уравнений отыскивается 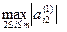, осуществляется сответствующую перестановка уравнений и т.д.

СхемаметодаГауссасвыборомглавногоэлементапострокамматрицы.

Перед исключением x₁ отыскивается 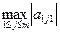. Пусть максимум достигается при j=j₀. Тогда поменяем взаимно номера у неизвестных x₁ и x_j0 (максимальный по величине из коэффициентов 1-го уравнения окажется в позиции a₁₁) и приступим к процедуре исключения x₁ и т.д.

СхемаметодаГауссас выбором главного элементаповсейматрице.

На 1-ом шаге среди элементов a_ij определяют максимальный по модулю элемент . 1-ое уравнение системы и уравнение с номером i₁ меняют местами и меняются взаимно номера у неизвестных x₁ и 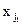(элемент окажется в позиции a₁₁). Далее стандартным образом производят исключение неизвестного 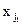из всех уравнений, кроме первого.

На k-ом шаге среди коэффициентов 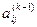при неизвестных в уравнениях системы с номерами 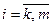выбирают максимальный по модулю коэффициент 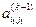. Затем k-ое уравнение и уравнение, содержащее найденный коэффициент, меняют местами и меняются взаимно номера у неизвестных x_k и 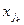(элемент окажется в позиции 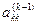). Исключается неизвестное 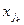из уравнений с номерами 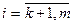. На этапе обратного хода неизвестные вычисляют в следующем порядке: .

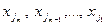Наиболее надёжным является метод исключения с выбором главного элемента по всей матрице коэффициентов на каждом шаге исключения. Рассмотренные модификации метода Гаусса позволяют, как правило, существенно уменьшить неблагоприятное влияние погрешностей округления на результаты расчёта.

Примеры.

Систему линейных уравнений, решённую нами методом Гаусса, решим с помощью его модификаций.

Решение.

1) Схемасвыборомглавногоэлементапостолбцам.

~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

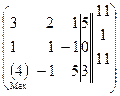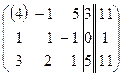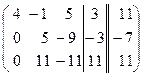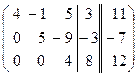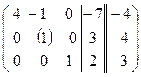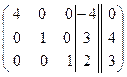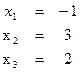
2) Схемасвыборомглавногоэлементапострокам.

~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

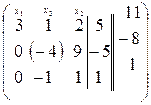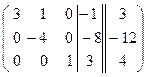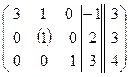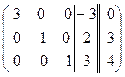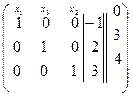
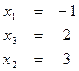
3) Схемасвыборомглавногоэлементаповсейматрице.

~ ~ ~ ~ ~ ~ ~ ~ ~ ~

~ ~ ~ ~

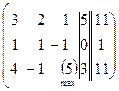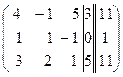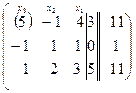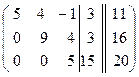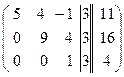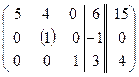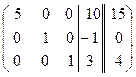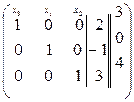
10. Метод полного исключения.

Данный метод используется для решения систем линейных уравнений, обращения матриц, разложения вектора по базису.

Алгоритм метода полного исключения

1-ыйшаг (соответствует исключению неизвестной x₁) выполняется с разрешающим элементом a₁₁¹0 по правилам прямого хода метода Гаусса.

Общийшаг (соответствует последовательному исключению неизвестных x₂, x₃,...) выполняется по следующим правилам:

1) назначается разрешающий элемент - им будет коэффициент при исключаемой неизвестной;

2) элементы разрешающей строки остаются неизменными;

3) все элементы разрешающего столбца (кроме разрешающего элемента) заменяются нулями и остаются таковыми до конца преобразований;

4) все прочие элементы пересчитываются по правилу прямоугольника.

Контроль вычислений осуществляется по суммарному столбцу.

Решим ту же самую СЛУ методом полного исключения.

~ ~ ~

~ ~ ~

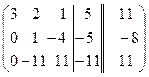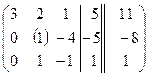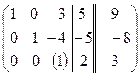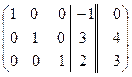
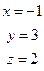
Вычислениеобратнойматрицыметодомполногоисключения.

Дана матрица 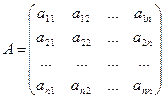, det A ¹0.

Составляем расширенную матрицу, приписав справа к исходной матрице единичную матрицу, отделив её от исходной вертикальной чертой:

.

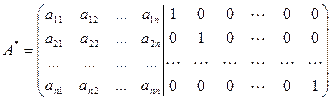Эта матрица подвергается преобразованиям по алгоритму полного исключения и слева от вертикальной черты получается единичная, а справа - обратная матрица А^-1. При расчёте желательно вести контроль вычислений.

Пример. Для матрицы А = 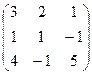найти А^-1, пользуясь методом полного исключения.

Решение.

~ ~

~ ~ ~

~ ~

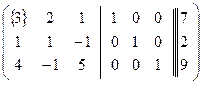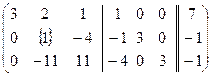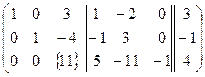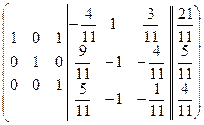
А^-1= =

Поиск по сайту: