АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Свойства определителя n-го порядка

Читайте также:
  1. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  2. Алгебраические свойства векторного произведения
  3. АЛГОРИТМ И ЕГО СВОЙСТВА
  4. Аллювиальные отложения и их свойства
  5. Апериодическое звено второго порядка.
  6. АТМОСФЕРА И ЕЕ СВОЙСТВА
  7. Атрибуты и свойства материи
  8. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
  9. Биосинтез белка и нуклеиновых кислот. Матричный характер реакций биосинтеза. Генетическая информация в клетке. Гены, генетический код и его свойства
  10. Валентные свойства атомов
  11. Валериана лекарственная - лечебные свойства, рецепты
  12. Виды подшипников качения и их свойства

1) Если какая-либо строка (столбец) матрицы А состоит из одних нулей, то det A=0.

2) При перестановке двух строк (столбцов) матрицы её детерминант меняет знак на противоположный.

3) Если матрица А содержит 2 одинаковые строки (столбца), то det A=0.

4) Общий множитель любой строки (столбца) можно выносить за знак детерминанта.

5) Если элементы двух строк (столбцов) матрицы А пропорциональны, то det A = 0.

6) Линейность детерминанта. Если каждый элемент некоторой строки (столбца) детерминанта 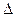представлен в виде суммы двух слагаемых, то этот детерминант равен сумме двух детерминантов, в каждом из которых:

a) все строки (столбцы), за исключением указанной строки (столбца), совпадают с аналогичными строками (столбцами) детерминанта ;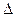

b) на месте указанной строки (столбца) 1-ый детерминант содержит первые слагаемые, а 2-ой детерминант – второе слагаемое данной строки (столбца) детерминанта .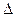

 

 

или

 

 

7) Детерминант матрицы не изменится, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

8) det A = det A .

9) Детерминанты треугольных и диагональной матриц равны произведению элементов главной диагонали.

 

Теорема Лапласа и использование свойств детерминанта лежат в основе так называемого метода накоплениянулей вычисления детерминанта.

 

Пример. Вычислить определитель

Решение:

3. Операции над матрицами.

Определение. Произведением матрицы 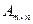на число 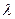называется матрица , элементы которой

Пример.

Матрица называется скалярнойматрицей.

Определение Суммой двухматриц A и В одинакового размера m´n называется матрица , элементы которой .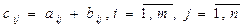

Пример.

 

Разностьдвухматриц одинакового размера mxn определяется через предыдущие операции: A – B = A + (-1)×B.

Пример.

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)