Область работоспособности определяется как область изменения диагностических признаков, ограниченная их допустимыми значениями, в которых объект работоспособен

Допустим нижние или верхние значения можно определить из анализа диагностической модели или воспользоваться приближенным расчетом:

где 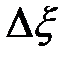– запас относительно предельного значения признака 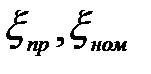– номинальное значение диагностического признака; k – коэффициент запаса.

В выражении не учитывается влияние множества случайных факторов, воздействующих на объект. Если состояние объекта диагностирования характеризуется совокупностью диагностических признаков, то условие работоспособности может быть задано в пространстве диагностических признаков, исходя из следующих предложений:

1.Определено множество состояний объекта S, т.е. совокупность диагностических признаков Θ.

2.Существуют номинальные лучшие состояния, т.е. определены Θ_НОМ.

3.Отклонения работоспособных состояний от номинальных допускаются в определенных пределах , соответствующих диапазону (н - нижнее, в- верхнее значение).

Таким образом, для всех точек в области работоспособности объект диагностирования приемлем для пользователя.В связи с тем, что в качестве диагностических признаков могут использоваться параметры и характеристики, задание условий работоспособности может осуществляться различными способами.

Если в качестве диагностических признаков используются параметры, то условия работоспособности по одному параметру, заданные неравенствами, ограничивающими значения с одной стороны, могут иметь вид:

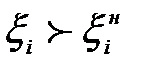(, сопротивление изоляции более 50 МОм);

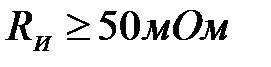(, сопротивление изоляции не менее 50 МОм);

(, сопротивление изоляции менее 50 МОм);

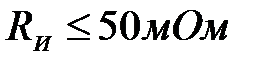(, сопротивление изоляции не более 50 МОм);

В большинстве случаев на диагностические параметры задаются двусторонние ограничение вида .

Если состояние объекта диагностирования определяется несколькими параметрами, т.е. , то задачу контроля работоспособности сводят к проверке указанных неравенств для каждого параметра. Если хотя бы одно из неравенств не выполняется, то объект признается неработоспособным.

Если в качестве диагностических признаков рассматривается характеристика y=f(x), где x и y соответственно входная и выходная переменные, то условия работоспособности определяются значениями отклонений текущей характеристики f(x) объекта от номинальной . При этом необходимо установить количественный критерий, который позволял бы оценивать сходство и различие этих характеристик.

Таких критериев существует несколько:

а ) критерий среднего отклонения

.

Интеграл в этом выражении численно равен площади фигуры, ограниченной функциями f(x) и (рисунок 2).

Рисунок 2

Недостатком этого критерия является одинаковая чувствительность, как к величине абсолютного отклонения, так и к длительности интервала, на котором оценивается отклонение.

б) Критерий среднеквадратичного отклонения

Этот критерий более чувствителен к величине, чем к длительности интервала, на котором отклонение оценивается. Он наиболее часто используется на практике.

в) Критерий равномерного приближения

В этом случае критерием близости является максимальное их отклонение на интервале [a,b]. Если максимальное отклонение мало, то на всем интервале определения функции будут мало отличаться друг от друга.

В этих случаях условие работоспособности будет выражено неравенством:

,

где E – допустимые отклонения; p=1,2,3 – вид критерия.

Допустимое отклонение на всю характеристику может задаваться в виде маски (рисунок 3).

Рисунок 3 – Маска

В случае, если характеристика оценивается по точкам (рисунок 4), области допустимых отклонений задаются для ограниченной совокупности точек на рабочем участке характеристики .

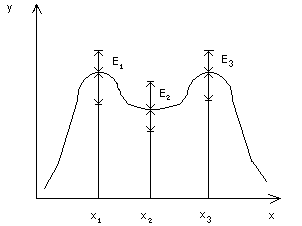
Рисунок 4 – Оценивание характеристики по точкам

Условия работоспособности задаются для каждой точки в виде неравенства . Если неравенства справедливы для всей совокупности рассматриваемых точек характеристики, то объект признается работоспособным.

Для объекта диагностирования состоящего из нескольких составных единиц, вектор состояния имеет вид . Условием работоспособности такого объекта является работоспособность каждой составной единицы. Состояние составной единицы может быть двух видов: работоспособна – 1, неработоспособна – 0. В этом случае условие работоспособного состояния сложного объекта можно представить в виде . Для каждой составной единицы условия работоспособности могут записываться в одном из приведенных выше видов.

Поиск по сайту: