 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методы, основанные на показателях надежности
Строить алгоритм поиска дефектов можно на основе известных показателей надежности, в качестве которых используются показатели безотказности (вероятности отказа qi или безотказной работы Pi) и ремонтопригодности (время, затрачиваемое на обнаружение дефекта  ). Возможны три способа:
). Возможны три способа:
· по показателям безотказности;
· по показателям ремонтопригодности;
· по отношению 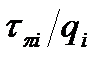 (“время – вероятность”).
(“время – вероятность”).
Для построения алгоритмов поиска дефектов необходимо знать показатели qi, для каждой структурной единицы объекта, i=1, n.
Алгоритм поиска дефекта на основании известных значений вероятности отказа qi структурных единиц.
При построении алгоритма поиска дефекта вводятся допущения:
· длительности всех проверок равны;
· отказы структурных единиц независимы;
· одновременно отказывает только одна (любая) структурная единица.
В этом случае алгоритм поиска может быть последовательным. Для его реализации вероятность отказа qi упорядочиваются по величине, и последовательно выполняются проверки, начиная со структурной единицы, характеризуемой наибольшей, и заканчивая структурной единицей, характеризуемой наименьшей величиной qi.
В качестве примера рассмотрим объект диагностирования, состоящий из 4-х структурных единиц, с известными вероятностями отказов qi: q1=0,6; q2=0,1; q3=0,18; q4=0,12. После ранжирования по величинам q1, получаем следующий порядок: q1, q3, q4, q2. Этот порядок определяет структуру алгоритма поиска дефектов (рисунок 4).
Рисунок 4 – Алгоритм поиска дефектов
Если имеется информация о времени, затрачиваемом на поиск дефекта каждой структурной единицы, то можно построить алгоритм поиска по правилу минимума временных затрат. Зная значения  , проверку надо начинать со структурной единицы, на поиск дефекта которой затрачивается наименьшее время и далее в порядке возрастания.
, проверку надо начинать со структурной единицы, на поиск дефекта которой затрачивается наименьшее время и далее в порядке возрастания.
Для объекта диагностирования, состоящего из 3-х структурных единиц с временем, затраченным на поиск дефекта соответственно:  ;
; 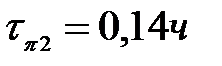 ;
;  .
.
Алгоритм поиска дефекта имеет вид, показанный на рисунке 5.
Рисунок 5 – Алгоритм поиска дефектов
Метод «Время - вероятность» является наиболее совершенным, так как учитывает два показателя. В этом случае последовательность проверок должна удовлетворять условию, согласно которому номер проверки определяется отношением 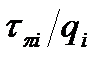 и возрастает с увеличением отношения.
и возрастает с увеличением отношения.
Для объекта диагностирования, имеющего дефект, состоящего из пяти структурных единиц, с вероятностями отказа соответственно: q1=0,05; q2=0,15; q3=0,3; q4=q5=0,25, время, затрачиваемое на поиск дефекта составляет соответственно: 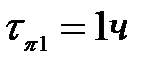 ;
; 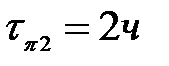 ;
; 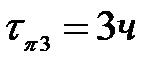 ;
;  ;
;  .
.
Для построения алгоритма поиска дефектов, соотношения 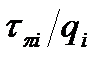 будут равны:
будут равны:  ;
; 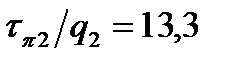 ;
; 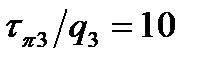 ;
; 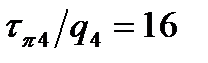 ;
;  .
.
Алгоритм поиска дефектов представлен на рисунке 6.
Рисунок 6 – Алгоритм поиска дефектов
Неопределенность в проверке может быть снята выбором либо показателя ремонтопригодности, либо безотказности. Рассмотренные методы не позволяют учесть взаимосвязи между структурными единицами, т.е. структуру объекта диагностирования.
Информационные методы
Предположим, что отказы всех структурных единиц, последовательно соединенных, равновероятны и образуют полную группу событий:
 .
.
где n – число возможных состояний (дефектов).
Каждая из проверок имеет только два исхода 1 или 0. Перед началом поиска состояний объекта диагностирования характеризуется максимальной энтропией (мерой неопределенности):
 ;
;
Каждая проверка πk дает определенное количество информации о состоянии объекта:  , где
, где 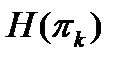 - средняя условная энтропия состояния объекта при выполнении проверки πk.
- средняя условная энтропия состояния объекта при выполнении проверки πk.
Поскольку для проверки πk возможны только два исхода (1 или 0) с вероятностями p(πk) и  соответственно, то
соответственно, то 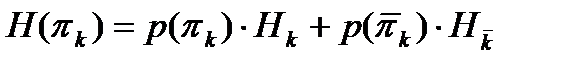 , где
, где 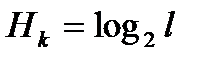 и
и  - энтропия состояния объекта после проведения проверки πk;
- энтропия состояния объекта после проведения проверки πk; 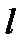 - число обнаруживаемых проверкой дефектов.
- число обнаруживаемых проверкой дефектов.
Тогда  и количество информации
и количество информации 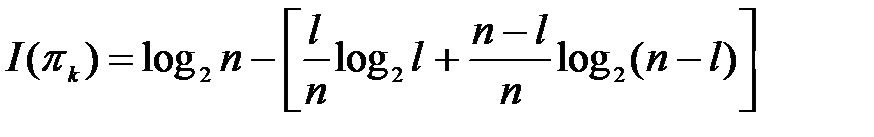 .
.
При построении алгоритма первой выбирается проверка πk, несущая максимум информации (если таких проверок больше одной, то выбирается любая из них), т.е. 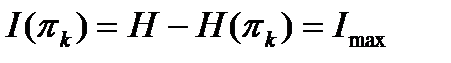 .
.
Второй выбирается проверка πk, которая обладает наибольшей условной информацией 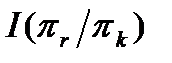 относительно состояния, характеризуемого энтропией
относительно состояния, характеризуемого энтропией 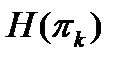 ,
,
 ;
;
 ;
;  ;
;  ;
;  ;
; 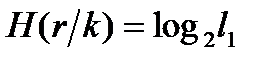 ;
;  ;
;  ;
;  ;
;
где  - число обнаруживаемых дефектов;
- число обнаруживаемых дефектов; 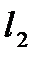 - число не обнаруживаемых дефектов.
- число не обнаруживаемых дефектов.
В этом случае:
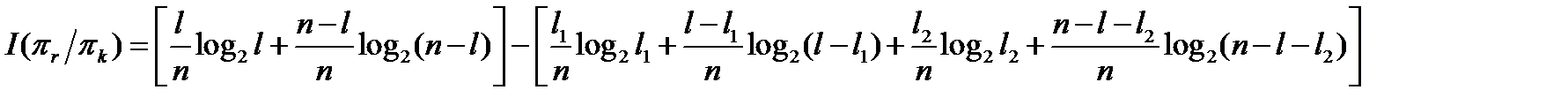
Третья и последняя проверка выбирается аналогичным образом. Процедура заканчивается тогда, когда энтропия  станет равна нулю.
станет равна нулю.
Простейшим примером метода является алгоритм половинного разбиения, при котором любая проверка снимает половину неопределенности. Если признаки наличия дефекта не дают основания считать какой либо элемент дефектным, то целесообразно первую проверку выполнить в контрольной точке, находящейся в середине схемы. Если результат проверки указывает на то, что сигнал в этой точке имеет допустимые значения, то из дальнейшего рассмотрения исключается первая половина схемы. Если в этой точке зафиксирован отрицательный результат, то дефект необходимо искать в первой половине схемы с последовательным соединением элементов. Процесс деления схемы пополам следует повторять до тех пор, пока не будет обнаружен последний дефект. Для объекта диагностирования, состоящего из 4-х элементов (рисунок 7а), алгоритм поиска дефекта, реализующий метод половинного разбиения, приведен на рисунке 7б.
Рисунок 7 – Алгоритм поиска дефекта
Недостаток информационного метода заключается в том, что может быть использован для объекта диагностирования, схемы которого сводятся к последовательному соединению элементов с равной вероятностью отказов.
Метод, основанный на анализе чувствительности функции передачи
Если диагностическая модель объекта диагностирования заданна в виде диаграммы прохождения сигналов вида (рисунок 8), то можно определить чувствительность функции передачи к изменению состояния элементов по выражениям:
 или
или 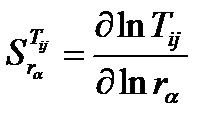
где Tij – функция передачи от i-го узла к j-му узлу; rα – изменяющиеся параметры, α=1, … 
Рисунок 8 – Диагностическая модель
Узлы диаграммы соответствуют переменным и обозначаются индексом соответствующего сигнала. Ветви имеют операторы, обозначенные соответствующей функцией передачи с указанием направления. Расположение узлов должно отражать распространение сигналов в объекте.
В реальном объекте функции передачи зависят от его структуры и значений параметров. Все изменения (количественные и качественные), происходящие в объекте, приводят к изменению соответствующих функций передач. В связи с этим различная чувствительность параметров определяется чувствительностью функции передач, которые находятся как степени их изменения при изменении какого либо параметра.
Обычно объект диагностирования характеризуется множеством функций передач. Их число определяется как сочетание:
 ,
,
где n – число параметров объекта диагностирования (если все параметры изменяются, то n=  ).
).
Сравнивая чувствительности, нужно упорядочить диагностические параметры по их влиянию на изменения состояния объекта, что составит алгоритм поиска дефектов. Анализ облегчится, если воспользоваться таблицей чувствительности функций передач.
| Функции передачи | Диагностические параметры | ||||
| r1 | … | rα | … | rl | |
| T0i | 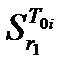
| … | 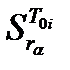
| … | 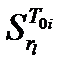
|
| … | … | … | … | ||
| … | … | … | … | ||
| … | … | … | … | ||
| Tij | 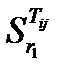
| 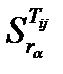
| … | 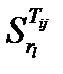
| |
| … | … | … | … | ||
| … | … | … | … | ||
| … | … | … | … | ||
| Tnm | 
| … | 
| … | 
|
Таблица 1
Каждый столбец этой таблицы представляет чувствительность функций передач к изменениям одного и того же параметра rα, каждая строка – чувствительность одной функции передачи к изменению каждого из параметров.
Для выбора последовательности проверок, составляющих алгоритм поиска дефектов, анализ таблицы сводится к сравнению строк. При этом осуществляется ранжирование вида  , если
, если 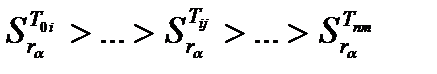 , где функция передачи T0i является наилучшей.
, где функция передачи T0i является наилучшей.
Далее анализируются строки с целью определения параметров, к которым функция передачи наиболее чувствительна. А эти параметры зависят от физических элементов, дефекты которых могут привести к их изменению. Упорядоченный ряд параметров rα по степени влияния на функции передачи объекта диагностирования определяет алгоритм поиска дефектов.
Поиск по сайту: