 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Математические модели дискретных устройств с памятью
Дискретные объекты с памятью – объекты, текущие значения выходных координат которых зависят не только от текущих значений их входных координат, но также от времени (от предыдущих входных воздействий).
В памяти дискретных объектов сохраняется информация о предыдущих входных воздействиях и реализуется физически либо при помощи специальных элементов памяти (например триггеров), либо путем организации контуров обратной связей, либо элементами временных задержек. Внутренние переменные дискретных объектов с памятью соответствуют обычно выходам триггеров, элементов, охваченных обратной связью, или элементов задержки. Совокупность значений выделенных внутренних переменных объекта с памятью в некоторый момент времени называют его внутренним состоянием.
Общепринятой математической моделью объекта является абстрактный или структурный конечный автомат. В конечном автомате всегда можно выделить комбинационную часть и память (рисунок 5).
Рисунок 5 – Конечный автомат
На рисунке 5 автомат приведен в однолинейном представлении, которое соответствует рассмотрению дискретного объекта с памятью как абстрактного конечного автомата.
При этом предполагается, что память автомата реализована на задержках, каждая из которых, обеспечивает запаздывание сигнала на одно и то же время. Если изменение значений входного сигнала происходит одновременно с изменением выходного сигнала памяти через интервалы времени  , то автомат называют синхронным, а интервал времени
, то автомат называют синхронным, а интервал времени  тактом синхронизации. В теории абстрактных автоматов принято называть внешний входной сигнал
тактом синхронизации. В теории абстрактных автоматов принято называть внешний входной сигнал  , внешний выходной сигнал
, внешний выходной сигнал  , выходной сигнал памяти
, выходной сигнал памяти  соответственно входным символом, выходным символом, символом внутреннего состояния (сокращенно состоянием).
соответственно входным символом, выходным символом, символом внутреннего состояния (сокращенно состоянием).
В соответствие с принятой идеализацией, функционирование исправного абстрактного конечного автомата может быть задано двумя зависимостями:

где  – символы входного, выходного и внутреннего состояний, индексы
– символы входного, выходного и внутреннего состояний, индексы  являются символами настоящего (текущего) и следующего такта. Задание автомата представленными зависимостями соответствует перечислению всех возможных пар входной сигнал-состояние и сопоставлению этим парам входных сигналов и состояний. Это может быть сделано в табличной, графической или матричной форме.
являются символами настоящего (текущего) и следующего такта. Задание автомата представленными зависимостями соответствует перечислению всех возможных пар входной сигнал-состояние и сопоставлению этим парам входных сигналов и состояний. Это может быть сделано в табличной, графической или матричной форме.
Функциональным описанием дискретного объекта является таблица переходов – выходов или эквивалентные ему описания в виде графа, матрицы переходов – выходов, таблицы истинности комбинационного эквивалента или системы булевых выходных функций и внутренних переменных.
Поведение объекта с памятью зависит не только от значений входов, но также от его состояний. Иными словами, один и тот же объект в ответ на одну и ту же входную последовательность может выдавать различные выходные последовательности в зависимости от того, в каком начальном состоянии находился объект в момент подачи первого входного символа рассматриваемой входной последовательности.При функциональном подходе состояния устройства исследователю неизвестны, так как внутренние переменные недоступны для наблюдения.
В качестве примера можно рассмотреть любую многотактную схему построенную на реле (рисунок 6). Работу многотактной схемы отображают при помощи таблицы переходов (ТП). Для ее построения составляют функции, описывающие схемы включения внутренних элементов памяти (реле Y1 и Y2) и выходную схему (включение лампы Z).
Для данной схемы:
 (2)
(2)
По полученной системе функций составляют кодированную таблицу переходов (таблица 6), которая содержит  столбцов (n – число видов схемы) и
столбцов (n – число видов схемы) и  строк (к – число внутренних элементов памяти). Каждый столбец соответствует одному из входных состояний схемы.
строк (к – число внутренних элементов памяти). Каждый столбец соответствует одному из входных состояний схемы.
Рисунок 6 – Многотактная схема
Таблица 6
| S | 
| x | |
| 00,0 | 01,0 | ||
| 11,1 | 01,1 | ||
| 11,1 | 10,1 | ||
| 00,0 | 10,0 |
В рассматриваемом случае возможны два входных состояния х=0 (кнопка х не нажата), и х=1 (кнопка х нажата). Строки соответствуют внутренним состояниям схемы, которые определяются состояниями ЭП. Представленная схема имеет 4 внутренних состояния: 00, 01, 10, 11. Каждому состоянию сопоставлено десятичное число  . На пересечении столбца и строки в клетке ТП указано внутреннее состояние, в которое переходит схема, если она находилась в состоянии, соответствующем данной строке, и на вход схемы поступил входной набор, соответствующий данному столбцу. Так из состояния
. На пересечении столбца и строки в клетке ТП указано внутреннее состояние, в которое переходит схема, если она находилась в состоянии, соответствующем данной строке, и на вход схемы поступил входной набор, соответствующий данному столбцу. Так из состояния  =00 под воздействием входной переменной х=0 схема переходит в состояние 00 (сохраняет свое состояние), а под воздействием входной переменной х=1 – в состояние 01.
=00 под воздействием входной переменной х=0 схема переходит в состояние 00 (сохраняет свое состояние), а под воздействием входной переменной х=1 – в состояние 01.
Состояния, в которых находится схема, вычисляются по уравнениям (2). Определяются значения функций  и
и  при подстановке переменных х,
при подстановке переменных х,  и
и 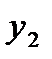 , соответствующих строке и столбцу, которым принадлежит элемент таблицы ТП, характеризующий данное состояние. В качестве примера можно вычислить состояние схемы, расположенное на пересечении столбца х=0 и строк
, соответствующих строке и столбцу, которым принадлежит элемент таблицы ТП, характеризующий данное состояние. В качестве примера можно вычислить состояние схемы, расположенное на пересечении столбца х=0 и строк  =01. После подстановки выбранных значений в функции получим:
=01. После подстановки выбранных значений в функции получим:
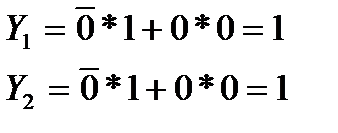
Для каждого состояния, расположенного в таблице, указывается значение выхода Z, которое рассчитывается аналогичным образом.
От кодированной ТП осуществляется переход к ТП, в которой внутренние состояния обозначаются цифрами (таблица 7), а от нее – к графу переходов (рисунок 7). В последнем вершины соответствуют состояниям схемы, а дуги – переходам между состояниями.
Таблица 7
| S | х | |
| 1,0 | 2,0 | |
| 3,1 | 2,1 | |
| 3,1 | 4,1 | |
| 1,0 | 4,0 |
Значение входа, под воздействием которого осуществляется переход, указывается над дугой.
Рисунок 7 – Граф переходов
Поиск по сайту: