Такого рода влияния и зависимости хорошо согласуются с понятием причинно-следственных связей, которые охватывают также строгие формальные зависимости между параметрами объекта

Графом причинно-следственных связей называют ориентированный граф, вершинами которого являются параметры, а дуги отражают причинно-следственные связи между вершинами. Направление дуги соответствует направлению перемещения от причины к следствию.

Графы причинно-следственных связей применяют для представления различных электрических, механических, комбинированных (например электромеханических) устройств, механизмов, машин и различных технологических процессов.

Логическая модель объекта может трактоваться как граф причинно-следственных связей между входными, внутренними и выходными параметрами объекта. При этом вершины графа соответствуют входным параметрам объекта и выходным параметрам блоков модели, а дуги – связям блоков между собой и с внешними входами объекта.

Модели в виде систем дифференциальных уравнений, диаграммы прохождения сигналов

Свойства динамических аналоговых объектов определяются дифференциальными уравнениями (линейными и нелинейными).

	=
	=

где – линейный оператор порядка ; 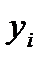и – выходная и входная функции соответственно.

Использование линейных дифференциальных уравнений в качестве диагностической модели позволяет сформулировать условия работоспособности в виде ограничений на реакцию объекта при стандартном входном воздействии, изменении значений коэффициентов уравнений и, в общем случае, при перемещении полюсов и нулей на комплексной плоскости. Однако для построения моделей в этом случае необходимо знать большое число параметров объектов, которые на этапе проектирования с достаточной точностью получить не удается. В связи с этим на практике часто ограничиваются рассмотрением зависимостей (передаточных функций) между некоторыми, представляющими наибольший интерес, входами и выходами объекта.

В ряде случаев в качестве диагностической модели можно рассматривать характеристическое уравнение: , и анализировать только изменение коэффициентов или полюсов (i=1,n). Известно, что полюсы определяют характер изменения выходного сигнала во времени и величины собственных частот объекта, а нули определяют относительную величину составляющих выходного сигнала.

Если характеристическое уравнение высокого порядка, то с целью упрощения вычислений используют для анализа эквивалентное уравнение более низкого порядка. Для того, чтобы сохранить существующие связи между коэффициентами уравнений и параметрами объекта, эквивалентное уравнение получают «усечением», т.е. простым устранением ряда членов при условии эквивалентности по определяющим корням уравнения.

Поиск по сайту: