В движущейся системе отсчета время течет медленнее

Экспериментальное доказательство явления замедления времени

Распад p⁺- мезона на m ⁺- мезон и нейтрино: p⁺→ m ⁺+ n.

Среднее время жизни p⁺- мезона (пиона) в собственной системе отсчета (т.е. в системе отсчета, в которой он покоится) равно t ₀ = 2.5×10^-8 с. В опытах, выполненных в 1952 г., были образованы пучки p⁺- мезонов, для которых , т.е. скорость p⁺-мезонов была близка к скорости света.

Время жизни пионов в лабораторной системе отсчета (в которой они движутся):

(, - последним слагаемым пренебрегаем).

Как измерить экспериментально?

Пучки пионов движутся со скоростью . Если бы не существовало явления замедления времени, то до распада пучок проходил бы расстояние

с)(3×10¹⁰см/с) =7.5×10² см=7.5 м.

Измеренный путь пучка:

=750 м, что соответствует 2.5×10^-6с - в соответствии с предсказанием СТО.

Следствие 3

Инвариантность интервала

(иметь представление о следствии и ходе рассуждений)

РИС. 4п-5

Мысленный эксперимент

В начальный момент времени 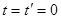, когда по условию оба начала отсчета совпадают, в общем начале отсчета проведем вспышку света. В обеих ИСО, 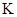и , свет распространяется по всем направлениям с одинаковой скоростью. Следовательно, в обеих ИСО волновой фронт будет сферическим.

Запишем уравнения сферы:

В системе	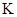В системе

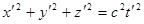
Мы знаем теперь, что в системах 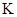и время течет по-разному, значит радиусы сфер (волновых фронтов) будут разными в разных системах отсчета, так что

, или

, или

Итак, в данном мысленном эксперименте речь идет о двух событиях:

1) отправление светового сигнала из точки (конкретно, из точки );

2) приход светового сигнала в другую точку .

Общее определение интервала:

координаты события 1 - ;

координаты события 2 - .

Введем обозначение интервала - или .

Основным свойством интервала между событиями является его инвариантность относительно перехода от одной ИСО к другой ИСО.

В неподвижной системе отсчета :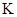

.

В движущейся системе отсчета :

(пользуемся преобразованиями Лоренца, вывод можно пропустить, но нужно знать последовательность математической операции)

= =

= = =

- что и требовалось доказать.

Рассмотрим плоскость и события, происходящие в этой плоскости. Введем новую переменную - расстояние, которое свет проходит за время .

РИС. 4п-5а

Геометрическая интерпретация преобразований Лоренца

РИС. 4п-6

 

Начала отсчета систем 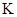, совпадают, так как, согласно преобразованиям Лоренца, из условия 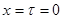следует .

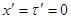Ищем положение оси . Определением этой оси является условие . Подставляем в преобразование Лоренца: .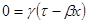

Отсюда - это уравнение оси .

Следовательно, ось повернута относительно оси на угол 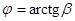против часовой стрелки. При 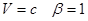, и угол поворота .

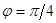Положение оси 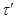определяется из условия : .

Уравнение оси 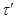: - ось повернута относительно оси на угол 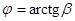по часовой стрелке. При 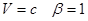, и угол поворота 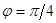. По биссектрисе распространяется свет.

 

Вывод

Преобразования Лорентца соответствуют переходу от прямоугольной системе координат к косоугольной системе .

 

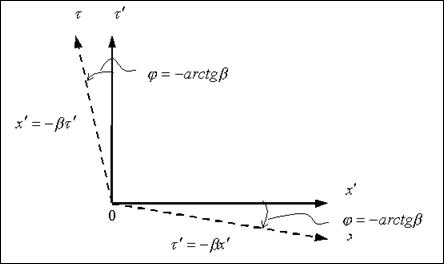Переход :

 

 

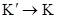РИС. 4п-7

Поиск по сайту: