АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Переходим к определению некоторых соотношений между этими коэффициентами

Читайте также:
  1. D) постоянных затрат к разнице между ценой реализации продукции и удельными переменными затратами.
  2. I Раздел 1. Международные яиившжоши. «пююеям как процесс...
  3. I. О различии между чистым и эмпирическим познанием
  4. II. Типы отношений между членами синтагмы
  5. III. Разрешение споров в международных организациях.
  6. IV. О различии между аналитическими и синтетическими суждениями
  7. Анализ взаимосвязей между показателями эффективности инвестиционно-инновационных проектов и показателями эффективности хозяйственной деятельности предприятия
  8. Анализ взаимосвязи между обобщающими, частными показателями экономической эффективности деятельности предприятия и эффективностью каждого научно-технического мероприятия
  9. Анализ затрат с учетом международных стандартов
  10. Анализ равновесия между активами предприятия и источниками их формирования. Оценка финансовой устойчивости предприятия
  11. Анализ стратегических альтернатив международной деятельности
  12. Анализ функциональной связи между затратами, объемом продаж и прибылью. Определение безубыточного объема продаж и зоны безопасности предприятия

(Необходимо знание общего принципа определения коэффициентов.)

 

1) Рассмотрим движение начала координат системы K’, т.е. точки . При этом в силу назначенного направления движения системы K’; по той же причине можем полагать . Получаем: .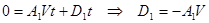

2) Если , то и при любых и . Следовательно, . Получаем: .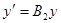

3) Если , то и при любых и . Следовательно, . Получаем: .

4) В силу изотропности пространства оси и равноправны, их можно поменять местами. Из этого следует: .

Осталась система уравнений:

6 неизвестных коэффициентов в правой части.

 

Теперь воспользуемся постулатом о постоянстве скорости света в любой ИСО: сферическая волна в любой ИСО.

Напоминание

Уравнение сферы радиуса : ; центр сферы находится в начале координат.

Итак, если световая волна распространяется из начала координат и начала она распространяться в момент времени 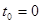, то в произвольный момент времени радиус волновой поверхности есть .

Уравнение сферической волны:

.

Условие сферичности волны в любой ИСО:

.

Отсюда видно, что время относительно, так как в противном случае получится, что имеются две одинаковые сферы с центрами в двух различных точках пространства, что бессмысленно.

Подставляем полученные выше выражения для в это соотношение:

Приравниваем коэффициенты при равных степенях переменных:


 

 

Коэффициент при Слева   Справа   Номер уравнения
1 = 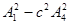(1)
1 = (2)
1 = (3)
= (4)
0 = (5)
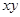
0 = (6)
0 = 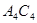(7)
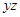
0 = (8)
0 = 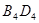(9)
0 = (10)

 

Таким образом, для определения 6 неизвестных коэффициентов мы получили 10 уравнений; значит, эти уравнения не независимы.


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)