АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Какие между ними связи?

Читайте также:
  1. D) постоянных затрат к разнице между ценой реализации продукции и удельными переменными затратами.
  2. I Раздел 1. Международные яиившжоши. «пююеям как процесс...
  3. I. О различии между чистым и эмпирическим познанием
  4. II. Типы отношений между членами синтагмы
  5. III. Разрешение споров в международных организациях.
  6. IV. О различии между аналитическими и синтетическими суждениями
  7. А какие болезни йога лечит?
  8. Анализ взаимосвязей между показателями эффективности инвестиционно-инновационных проектов и показателями эффективности хозяйственной деятельности предприятия
  9. Анализ взаимосвязи между обобщающими, частными показателями экономической эффективности деятельности предприятия и эффективностью каждого научно-технического мероприятия
  10. Анализ затрат с учетом международных стандартов
  11. Анализ равновесия между активами предприятия и источниками их формирования. Оценка финансовой устойчивости предприятия
  12. Анализ стратегических альтернатив международной деятельности

1) Из (2) и (3) следует, что .

2) Из (8) следует, что 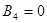или , или . Поскольку , то получаем . Тогда . Знак минус соответствует повороту осей на 1800, и вследствие изотропности пространства это не имеет физического смысла. Выбираем .

3) Поскольку в уравнения (6)-(10) входят справа или , или , то они удовлетворяются тождественно и интереса не представляют.

 

Осталось три уравнения:

Из уравнения (5) находим: .

Подставляем в (4):

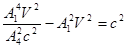Þ Þ .

Полученное подставляем в (1):

Þ Þ

Þ Þ

(знак плюс выбираем из физических соображений – изотропия пространства).

Отсюда сразу находим закон преобразования пространственных координат:

; ; .

Подставляем значение в уравнение (4):

.

Делим на и находим :

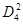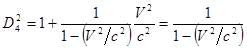Þ

.

Подставляем полученное значение и А1 в ранее полученное выражение (5) и находим :

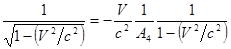Þ

.

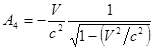Находим закон преобразования временной координаты:

.

 

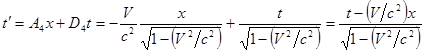Итак, получены преобразования Лоренца:

 

K K’ K’ K

 

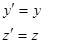
Обычно вводят обозначения 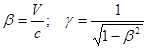. Тогда:

K K’ K’ K

 

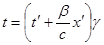
Преобразования Лоренца обеспечивают инвариантность уравнений Максвелла при переходе от одной ИСО к другой.

При « 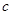преобразования Лоренца переходят в преобразования Галилея (), т. е. удовлетворяют принципу соответствия.

 

 

Примечание Уравнение Шредингера неинвариантно относительно преобразований Лоренца

 


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)