Второе важное обстоятельство - преобразования Галилея меняют вид уравнений Максвелла

РИС. 4-9

В системе фотоэлементы ФЭ1 и ФЭ2 сработают одновременно.

В неподвижной системе отсчета 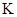фронт световой волны будет по-прежнему
(как и в ) сферическим. Поскольку ФЭ1 приближается к источнику, а ФЭ2 удаляется от него, сначала сигнал регистрирует ФЭ1, потом ФЭ2.

События, которые происходили одновременно в , сделались неодновременными в .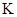

Второе важное обстоятельство - преобразования Галилея меняют вид уравнений Максвелла

(уравнения Максвелла неинвариантны относительно преобразований Галилея).

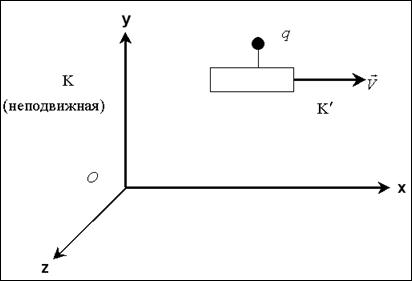
РИС. 4-10

Заряд q в системе покоится – следовательно, в этой системе он создает лишь электростатическое поле; в системе 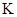этот заряд движется. Движение заряда эквивалентно протеканию тока и, значит, приводит к возникновению магнитного поля.

Итак, один и тот же заряд q:

- в системе создает лишь электростатическое поле,

- в системе 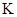создает постоянное магнитное поле.

Этот результат противоречит принципу эквивалентности ИСО (первому постулату Эйнштейна).

Задача, которую решил Г. А. Лоренц (1853-1928):

найти преобразования координат (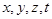) – такие, чтобы уравнения Максвелла были инвариантны относительно этих преобразований.

Правильность полученных преобразований должна быть подтверждена инвариантностью законов Ньютона, основ термодинамики, законов сохранения, а также всеми следствиями из этих преобразований.

Преобразования Лоренца

РИС. 4-11

Пусть даны координаты события в системе K: .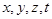

Ищем координаты события в системе K’: .

В силу однородности пространства преобразования должны быть линейными:

16 неизвестных коэффициентов в правой части.

Поиск по сайту: