 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
D - разбиение по двум параметрам
|
Читайте также: |
В основе лежит допущение, что в характеристическом уравнении можно выделить два параметра, М и N, которые могут изменяться, а остальные параметры заданы. Параметром может быть коэффициент или комбинация коэффициентов.
Если параметры М и N входят в характеристическое уравнение линейно, то характеристическое уравнение может быть представлено в виде
MQ (p) + NR (p) + H (p)=0, (5.7)
где Q, R, H – некоторые полиномы.
Выделение областей устойчивости в плоскости параметров N и М достигается следующей процедурой.
Подставляем в характеристическое уравнение p = jω. Полиномы Q, R, H распадаются на вещественные и мнимые части:
Q (jω) = Q 1(ω) + jQ 2(ω),
R (jω) = R 1(ω) + jR 2(ω),
H (jω) = H 1(ω) + jH 2(ω).
Теперь их надо ввести в характеристическое уравнение (5.7) и выделить действительные и мнимые слагаемые:
[ Q 1(ω) М + R 1(ω) N + H 1(ω)] + j [ Q 2(ω) M + R 2(ω) N + H 2(ω)] = 0.
Если комплексное выражение равно нулю, значит его действительное и мнимое слагаемые по отдельности равны нулю:
Q 1(ω) M + R 1(ω) N + H 1(ω) = 0,
Q 2(ω) M + R 2(ω) N + H 2(ω) = 0.
Получается два линейных уравнения для определения параметров M и N:
Q 1(ω) M + R 1(ω) N = - H 1(ω),
Q 2(ω) M + R 2(ω) N = - H 2(ω). (5.8)
Величины Q 1, Q 2, R 1, R 2 рассматриваются как коэффициенты, а М и N – как переменные.
Определитель системы
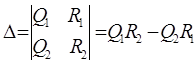 .
.
Определители параметра М и параметра N:
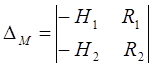 ,
, 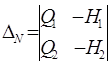 .
.
Определитель D М получается из определителя системы заменой элементов первого столбца свободными членами системы. Определитель D N – заменой элементов второго столбца свободными членами системы.
Для конкретного значения w:
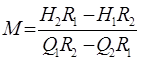 ,
, 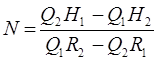 .
.
На плоскости M, N это будет точка. Задавая ω от нуля до бесконечности, в плоскости M, N можно построить кривую, которая и есть граница D - разбиения. Система уравнений (5.8) имеет решение, если Δ ≠ 0 и Δ M ¹ 0, Δ N ≠ 0; и не имеет решения, если Δ = 0 (точка с координатами (M, N) уходит в бесконечность). В случае Δ = 0, Δ M = 0, Δ N = 0, значения M и N становятся неопределенными. Уравнения (5.8) становятся зависимыми и определяют собой не точку, а прямую в плоскости M, N. Такая прямая называется особой прямой. В большинстве случаев особые прямые получаются для ω = 0 и ω = ∞.
Область устойчивости выделяется штриховкой. Правило штриховки следующее.
Если определитель Δ > 0, то двигаясь по D - кривой от ω = -∞ до ω = +∞, штрихуют левую сторону. Если Δ < 0, то штрихуют правую сторону (знак определителя меняется, если + ω заменить на - ω).
Поиск по сайту: