 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 5.14
Дано характеристическое уравнение вида:
 .
.
Требуется найти значения Т, при которых система будет устойчивой.
Назначив Т параметром, выделим  :
:
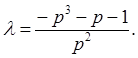
Полагая  получаем:
получаем:
 .
.
Запишем действительную и мнимую части:


Анализ формул показывает:
- при w = 0 U = ¥, V = ¥;
- при w = 1 U = 1, V = 0; кривая V (U) пересекает действительную ось;
- при w = ¥ U = 0, V = -¥;
Кривая начинается в +¥, пересекает ось абсцисс и неограниченно приближается к мнимой оси, уходя в -¥.
Для уточнения хода кривой V (U) можно взять точки:
w = 0,5, U = 4, V = 1,5.
w = 2, U = 0,25, V = -1,5;
 , U = 0,5 V = -0,7;
, U = 0,5 V = -0,7;
w = 0,82, U = 1,5, V = -0,4.
Построив на плоскости U, V кривую для положительных частот, отображаем ее зеркально относительно действительной оси и получаем кривую для отрицательных частот, рис. 5.26. Нанеся штриховку, получаем область устойчивости. Устойчивость системы обеспечивают те значения параметра l, которые располагаются на отрезке действительной оси от 1 до ¥. Контрольная проверка по критерию Гурвица подтверждает вывод.
 V
V
|
 w → - ∞ w → 0
w → - ∞ w → 0
 1.5
1.5





 1
1
 | ||||||||||||||||
 | ||||||||||||||||
 | ||||||||||||||||
 | ||||||||||||||||
 | ||||||||||||||||
 | ||||||||||||||||
 | ||||||||||||||||
 | ||||||||||||||||
 | ||||||||||||||||


 0.5
0.5
 | |||
 | |||









 2 3 4 U
2 3 4 U


 -0.5
-0.5
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||






 -1
-1
 | |
 | |
 |


 -1.5 w → 0
-1.5 w → 0
w → + ∞
Рис. 5.26
Дано характеристическое уравнение вида
 .
.
Требуется найти интервал значений параметра λ, при которых САР будет устойчивой.
Записав

и положив p = jω, получаем комплексный параметр λ в виде
 .
.
Выделяем действительную и мнимую части:
 ,
,  .
.
Задаем ω и рассчитываем U и V для построения кривой V (U):
| ω | U | V |
| ∞ | -∞ | |
| 2,36 | -6,7 | |
| 3,16 | ||
| 3,1 | 1,9 | |
| 2,4 | ||
| 5,45 | 1,68 | 2,44 |
| 1,4 | 2,4 | |
| 0,5 | 1,8 | |
| ∞ |
Построив кривую для положительных w, дополняем ее зеркально отображенной (для отрицательных ω). Результат показан на рис. 5.27.
 V
V
 3
3
 |




 2 w = - 0
2 w = - 0
 |








 2 U
2 U
w = - ∞ 






 | |||||||||
 |  | ||||||||
 |  | ||||||||







 -2 w = + 0
-2 w = + 0

-3
Рис.5.27.
Вывод: САР устойчива при значениях λ, принадлежащих интервалу
0 < l < 5. Границе устойчивости отвечают λ = 0 и λ = 5.
Контрольная проверка по критерию Гурвица: все коэффициенты характеристического уравнения больше нуля, определитель a 1 a 2 - a 0 a 3 > 0. 
Поиск по сайту: