АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 5.9

Читайте также:
  1. X. примерный перечень вопросов к итоговой аттестации
  2. В некоторых странах, например в США, президента заменяет вице-
  3. В примере
  4. Вания. Одной из таких областей является, например, регулирова-
  5. Вашим сообщениям, например, спеть «С днем рождения»
  6. Виды знания. Контрпример стандартному пониманию знания
  7. Власть примера. Влияние с помощью харизмы
  8. Внешний долг (внешняя задолженность): пример России
  9. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).
  10. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  11. Вопрос 8. Герои романтических поэм А. С. Пушкина (на примере одного произведения).
  12. Второй пример абстрактного синтеза

Система с передаточной функцией

замыкается. Будет ли она устойчивой?

Находим передаточную функцию замкнутой системы

.

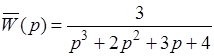Записываем характеристический полином замкнутой системы

D (p) = p 3 + 2 p 2 + 3 p + 4

и соответствующий ему комплексный частотный полином

D (jw) = - jw 3 - 2 w 2 + j 3 w + 4.

Его действительная и мнимая части:

U (w) = 4 - 2 w 2, V (w) = 3 w - w 3.

Определяем частоты пересечения, координаты точек пересечения, углы.

V (w) = 0. w 1 = 0, U (w) = 4, j (w) = 0.

w 3 = , U (w) = -2, j (w) = 2 (p/2).

U (w) = 0. w 2 = , V (w) = , j (w) = (p/2).

w = ¥ j (w) = -3(p/2).

Требование w 1 < w 2 < w 3 выполняется, углы последовательно возрастают, вектор D (jw) делает поворот на 3(p/2) радиан.

Вывод: система устойчивая.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)