 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 4.2. Неустойчивое звено с передаточной функцией
Неустойчивое звено с передаточной функцией

последовательно соединяется с неустойчивым звеном, имеющим передаточную функцию.
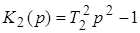 .
.
Выяснить, при каком условии система будет устойчивой.
Передаточная функция системы
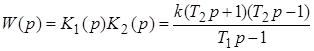 .
.
Если положить T 1 = T 2 , передаточная функция системы принимает вид: W (p) = k (T 2 p + 1). Передаточная функция не содержит знака «минус», что является признаком устойчивости. Значит, условие устойчивости системы T 1 = T 2.
Интегрирующее звено соединяется последовательно с реальным дифференцирующим звеном. Найти передаточную функцию.
Передаточные функции звеньев:
 и
и  .
.
Перемножая, получаем передаточную функцию соединения:
 ,
,
где k = k 1 k 2 / T 1 . Она оказалась передаточной функцией инерционного звена.
(Пример показывает, что инерционное звено можно заменить последовательным соединением интегрирующего и реального дифференцирующего звеньев).
Поиск по сайту: