Интегрирующее звено

Дифференциальное уравнение этого звена устанавливает пропорциональность скорости изменения выходной величины величине входного воздействия:

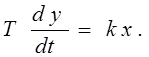(3.4)

(Сама выходная величина пропорциональна интегралу от входной величины,

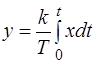
Операторное уравнение:

.

Передаточная функция:

.

Комплексная частотная характеристика

.

Действительная частотная характеристика U (w) = 0. Мнимая частотная характеристика V (w) = - k / Tw.

Амплитудная частотная характеристика

.

При w = 1 / T, амплитуда равна коэффициенту усиления. В области w < 1 / T амплитуда возрастает по мере уменьшения w и когда w = 0, становиться равной ∞. В области w > 1 / T амплитуда уменьшается с увеличением w и стремиться к нулю при неограниченном увеличении w.

Фазовая частотная характеристика от w не зависит:

, j = - 90°. Запаздывание по фазе постоянное при любой частоте.

Логарифмическая амплитудная частотная характеристика

.

В области низких частот w < 1 и в области высоких частот w > 1 вид функции один и тот же. Зависимость представляет собой прямую, которая пересекает ординату в точке с координатами lg w = 0, L (w) = 20 k / T и абсциссу в точке с координатами lg w = lg (k / T), L(w) = 0. Рис 3.5.

Логарифмическая фазовая частотная характеристика от частоты не зависит.

Переходная функция – прямая с уравнением

.

Рис. 3.5. Логарифмическая амплитудная частотная характеристика интегрирующего звена

Характеристиками интегрирующего звена обладают так называемые интегральные регуляторы (сокращенно И-регуляторы). Их применение позволяет снизить ошибку регулирования.

Поиск по сайту: