 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частотные характеристики
Передаточная функция выражает свойства системы через комплексную переменную, которая содержит действительную и мнимую части: p = s + jw. Мнимая часть имеет смысл циклической частоты колебаний. Если взять чисто мнимое значение комплексной переменной, p = jw, и ввести эту величину в передаточную функцию (2.6), получается частотная функция:
. (2.8)
Ее называют комплексная частотная характеристика, амплитудно-фазовая частотная характеристика, комплексный коэффициент усиления.
По определению, она записывается отношением частотных полиномов. Но возможны и другие формы записи. Обратим внимание на то, что частотный полином В (jw) в развернутом виде,
,
представляет собой сумму действительной и мнимой частей:
.
Так получается потому, что j = 
в четной степени будет либо –1, либо +1.
Частотный полином D (jw) в развернутом виде имеет ту же структуру:
D (jw) = D 1(w) + jD 2(w),
Следовательно комплексная частотная характеристика есть отношение двух комплексных чисел:
.
Умножение числителя и знаменателя на число, сопряженное знаменателю, позволяет выделить действительную и мнимую части:
.
Первое слагаемое обозначим U (w), второе V (w). U (w) называют действительной частотной характеристикой, V (w) - мнимой частотной характеристикой. В краткой записи
W (jw) = U (w) + jV (w). (2.9)
Комплексное выражение (2.9) можно интерпретировать геометрически, отложив по оси абсцисс действительную частотную характеристику, по оси ординат – мнимую частотную характеристику, рис. 2.1.
V (w)
М
A V
j
 |
0 U U (w)
Рис. 2.1.
Для заданной частоты U (w) и V (w) – пара чисел, определяющих положение точки М на плоскости. Соединив прямой А начало координат с точкой М, получим прямоугольный треугольник. Для него справедливы соотношения: 
, 
,
, 
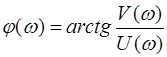. (2.10)
Все величины – функции частоты w.
Комплексную частотную характеристику, следовательно, можно записать в виде
W (jw) = U (w) + jV (w) = A (cos j (w) + j sin j (w)).
По формуле Эйлера 
. Поэтому
. (2.11)
А (w) называют амплитудной частотной характеристикой или просто амплитудой. j (w) называют фазовой частотной характеристикой или просто фазой.
Записать комплексную частотную характеристику, частотные характеристики, амплитуду и фазу для системы, описываемой дифференциальным уравнением
.
Преобразуя по Лапласу, получаем операторное уравнение
(p 2 + 3 p + 1) Y (p) = 2 X (p)
и передаточную функцию:
.
Подстановкой p = jw превращаем передаточную функцию в комплексную частотную характеристику:
.
Действительная частотная характеристика
.
Мнимая частотная характеристика
.
Амплитуда
.
Фаза
.
Найти комплексную частотную характеристику, амплитуду и фазу пропорционально-интегрального регулятора (ПИ-регу-лятора). Его уравнение
.
(T – постоянная времени, k – коэффициент усиления).
Продифференцируем исходное уравнение,
и преобразуем по Лапласу:
.
Из операторного уравнения составим передаточную функцию:
.
Полагая p = jw, записываем комплексную частотную характеристику
,
находим частотные характеристики:
U (w) = k, V (w) = - 
,
и амплитудную частотную характеристику:
.
Фаза в функции частоты имеет выражение
.
Найти логарифмическую амплитудную частотную характеристику ПИ-регулятора.
Воспользуемся выражением для амплитуды и запишем общий вид ЛАЧХ:
L (w) = 20 lg A (w) = 10 lg(k 2 T 2 w 2 + 1) – 20 lg Tw.
Выделим асимптотические прямые.
В области w < 1. С уменьшением w слагаемое k 2 T 2 w 2 становится пренебрежимо меньше единицы. Его можно отбросить. Тогда первый член L (w) обращается в нуль вследствие lg 1 = 0. Остается
L 1 = - 20 lg T – 20 lg w.
В области w > 1. В первом слагаемом следует пренебречь единицей. В таком случае
L 2 = 20 lg k + 20 lg Tw - 20 lg Tw = 20 lg k.
Для построения графика надо найти точки пересечения прямой L 1 c осями координат и с прямой L 2 . (По ординате откладывают L 1, L 2, по абсциссе lg w).
Точка пересечения с осью ординат находится из условия lg w = 0. Получается: L 1 = -20 lg T = 20 lg (1/ T).
Точка пересечения с осью абсцисс находится из условия L 1 = 0. Получается: lg w = lg (1 / T).
Точка пересечения прямой L 1 с прямой L 2 находится из условия L 1 = L 2 . Получается: lg w = lg (1 / kT).
Вид графика показан на рис. 2.1.
Рис. 2.2. Асимптотическая логарифмическая
амплитудная частотная характеристика ПИ-регулятора
Поиск по сайту: