АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Интегральные оценки качества

Читайте также:
  1. III. ДРУГИЕ ОЦЕНКИ КОЛЛЕКТИВНОЙ ДУШЕВНОЙ ЖИЗНИ
  2. III.4. Критерии оценки преступления. Вина
  3. Kритерии оценки новой продукции
  4. Алгоритм оценки погрешностей прямых измерений физических величин
  5. Анализ и оценки уязвимостей
  6. Анкета оценки уровня обучения студента курса «Системный анализ»
  7. Аудит состояния учета, оценки и сохранности остатков незавершенного производства
  8. Балльная оценка параметров инвестиционной привлекательности организаций и первичные параметры оценки. Метод интегральной оценки.
  9. Балльно-рейтинговая система оценки успеваемости
  10. Весовые коэффициенты для оценки факторов, определяющих привлекательность фирм-заказчиков
  11. Виды кислотности, методы определения и оценки
  12. Виды оценки основных фондов

 

Первая интегральная оценка:

. (6.8)

Чем меньше интеграл, тем выше качество регулирования.

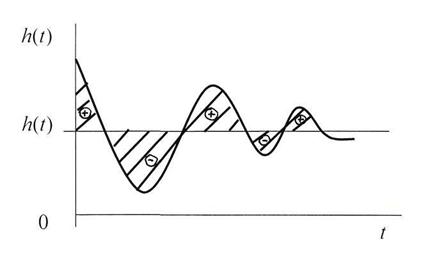
Однако, в случае колебательного переходного процесса интеграл (6.8) представляет собой алгебраическую сумму площадей, ограниченных кривой переходного процесса h (t) и прямой h = h (∞). Отдельные площади суммируются с разными знаками. Интеграл получается минимальным при неудовлетворительном переходном процессе, рис. 6.9. Интеграл (6.8) дает правильное представление о переходном процессе только в случае монотонного хода кривой (например, как на рис. 6.3).


 

 

Рис. 6.9. Площади, которые учитывает интеграл (6.8).

 

Вторая интегральная оценка:

. (6.9)

(Интегральная квадратичная ошибка регулирования).

Интеграл (6.9) тоже суммирует площади, расположенные над и под абсциссой h = h (∞). Но в силу квадратичности функции, все слагаемые положительные.

Чем меньше интеграл J 2, тем выше качество регулирования.

Преимущество интегральной оценки J 2 в том, что она применима к колебательным процессам.

Третья интегральная оценка учитывает плавность протекания процесса.

. (6.10)

τ – постоянная, имеющая размерность времени. Плавность измерения регулируемого параметра достигается за счетпроизводной dy / dt.

Третья интегральная оценка применима для характеристики как монотонного, так и колебательного процесса. Неудобство применения оценки (6.10) в том, что должно быть заранее известна постоянная τ.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)