Понятие об устойчивости

Система, которая после завершения переходного процесса приходит к состоянию установившегося равновесия, называется устойчивой. В устойчивой системе регулируемая величина со временем стремится к постоянному значению.

Система называется неустойчивой, если после устранения воздействия она удаляется от состояния равновесия или совершает около него недопустимо большие колебания. В неустойчивой системе регулируемая величина со временем возрастает.

Если заранее выяснить, будет ли регулируемая величина неограниченно возрастать после воздействия, можно получить ответ на вопрос об устойчивости системы.

Характер воздействия на систему и поведение управляемой величины описывается дифференциальным уравнением. Оно было записано для разомкнутой системы в главе 2:

(2.1)

Когда воздействие на систему прекращается, правая часть обращается в ноль и дальнейшее изменение управляемой величины описывается однородным дифференциальным уравнением

. (5.1)

Решение однородного уравнения показывает, возрастает или не возрастает со временем управляемая величина. Решение ищут, полагая y (t) = e ^pt. Беря производные и подставляя в уравнение (5.1) находят характеристическое уравнение

, (2.7)

решая которое, получают корни p_i. Полное решение уравнения (5.1) слагается из экспонент:

(5.2)

где С_i – постоянные интегрирования.

Функция y (t) – описывает переходной процесс; он полностью определяется значением корней p_i.

Корни характеристического уравнения могут быть действительными, комплексными, мнимыми. Если корни действительные и отрицательные, каждая экспонента со временем стремится к нулю, следовательно, y (t) ® 0. По окончании переходного процесса система приходит к состоянию установившегося равновесия.

Если корни действительные и положительные, все экспоненты со временем неограниченно возрастают, y (t) ® ¥. Процесс неустойчивый, система удаляется от состояния равновесия.

Если корни комплексно-сопряженные с отрицательной действительной частью, каждая экспонента со временем стремится к нулю, имея колебательную составляющую. И в этом случае y (t) ® 0. Система, следовательно, устойчивая.

В случае комплексно-сопряженных корней с положительной действительной частьюсистема неустойчивая.

При наличии чисто мнимых корней выходная величина совершает гармонические колебания. Мнимые корни соответствуют границе устойчивости.

Итак, система устойчива только в том случае, когда действительная часть корней характеристического уравнения отрицательная.

Для суждения об устойчивости необязательно решать дифференциальное уравнение. Как было показано в Главе 2, дифференциальному уравнению (2.1) соответствует передаточная функция

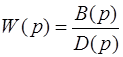, (2.6)

где ,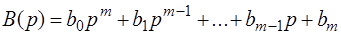

.

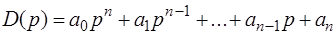Знаменатель передаточной функции – характеристический полином. Будучи приравнен нулю, он дает характеристическое уравнение:

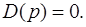(5.3)

Дифференциальные уравнения (2.1), (5.1) и передаточная функция (2.6) описывают разомкнутую систему, следовательно, характеристическое уравнение (5.3) тоже относится к разомкнутой системе.

Зная передаточную функцию разомкнутой системы W (p), можно записать передаточную функцию замкнутой системы:

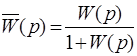. (4.6)

Заменяя W (p) по формуле (2.6), получаем:

. (5.4)

Знаменатель – характеристический полином замкнутой системы.

Сравнивая формулы (5.7) и (2.6), по аналогии заключаем, что уравнение

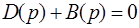. (5.5)

представляет собой характеристическое уравнение замкнутой системы. Поделив (5.5) на D (p),получаем характеристическое уравнение замкнутой системы, выраженное через передаточную функцию разомкнутой системы:

. (5.6)

Формулы (5.3), (5.5), (5.6) дают возможность судить об устойчивости разомкнутой или замкнутой системы автоматического регулирования.

Дано дифференциальное уравнение разомкнутой системы:

Найти характеристическое уравнение и его корни.

Поиск по сайту: