АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 2.1. Записать передаточную функцию и характеристическое уравнение для системы, поведение которой описывается дифференциальным уравнением

Читайте также:
  1. X. примерный перечень вопросов к итоговой аттестации
  2. В некоторых странах, например в США, президента заменяет вице-
  3. В примере
  4. Вания. Одной из таких областей является, например, регулирова-
  5. Вашим сообщениям, например, спеть «С днем рождения»
  6. Виды знания. Контрпример стандартному пониманию знания
  7. Власть примера. Влияние с помощью харизмы
  8. Внешний долг (внешняя задолженность): пример России
  9. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).
  10. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  11. Вопрос 8. Герои романтических поэм А. С. Пушкина (на примере одного произведения).
  12. Второй пример абстрактного синтеза

Записать передаточную функцию и характеристическое уравнение для системы, поведение которой описывается дифференциальным уравнением

,

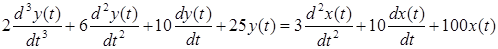Производим замену символов в дифференциальном уравнении:

на p, p 2, p 3 ;

y (t) на Y (p);

x (t) на X (p).

 

Получаем операторное уравнение:

(2 p 3 + 6 p 2 +10 p +25) Y (p) = (3 p 2 + 10 p +100) X (p).

Отношение Y (p) / X (p) есть передаточная функция W (p). Значит, искомая передаточная функция есть

.

 

Комплексные полиномы имеют вид:

В (p) = 3 p 2 + 10 p + 100,

D (p) = 2 p 3 + 6 p 2 + 10 p +25.

Характеристическое уравнение получается, если приравнять нулю комплексный полином знаменателя передаточной функции:

2 p 3 + 6 p 2 + 10 p + 25 = 0.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)