Математические модели входных воздействий

В дифференциальном уравнении (2.1) правая часть есть сумма воздействующего на вход системы сигнала x (t) и его производных. В реальных условиях на вход системы воздействуют сигналы произвольного характера. То есть, математически они описываются произвольными зависимостями входной величины от времени. Однако, в теоретических исследованиях принимают, что воздействия оказываются в виде единичного скачка, единичного импульса, гармонического колебания, сигнала постоянной скорости. Эти воздействия называют типовыми.

Ступенчатая функция (единичный скачок). В момент t = 0 воздействиемгновенно достигает величины x = 1, далее со временем не меняется. График показан на рис. 2.3.

Единичную ступенчатую функцию записывают символом 1(t).

t < 0 1(t) = 0,

t = 0 1(t) = 1,

t > 0 1(t) = 1.

Если воздействие ступенчатое, но отличается от единичного в А раз, его обозначают А(1). А(1) = А1(t).

Импульсная функция (единичный импульс). Это такой импульс величина которого равна бесконечности, длительность - нулю, а площадь – единице. В математике известен как дельта функция. Обозначается .

t < 0 d(t) = 0,

t = 0 d(t) = ¥,

t > 0 d(t) = 0.

Единичный импульс есть производная от единичной ступенчатой функции:

Импульсную функцию можно трактовать как предел прямоугольного импульса, у которого высота стремится к ¥, а время его действия – к нулю.

Гармоническая функция. Это функция, изменяющаяся по закону синуса или косинуса.

Записывается либо как

либо как .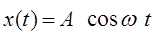

Величина воздействия колеблется между значениями A и -A.

Поиск по сайту: