АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Системы. Система, в структуре которой нет последовательно присоединенного интегрирующего звена, называется статической

Читайте также:
  1. I. Формирование системы военной психологии в России.
  2. II. Цель и задачи государственной политики в области развития инновационной системы
  3. II. Экономические институты и системы
  4. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  5. SCADA-системы
  6. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  7. TRACE MODE 6: компоненты инструментальной системы
  8. А). Системы разомкнутые, замкнутые и комбинированные.
  9. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство
  10. Абиотические компоненты экосистемы.
  11. Абстрактные линейные системы
  12. Автоматизированные системы контроля за исполнением документов

Система, в структуре которой нет последовательно присоединенного интегрирующего звена, называется статической. Примером может служить последовательное соединение звеньев с передаточными функциями

, , .

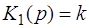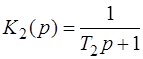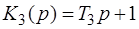Передаточная функция системы имеет вид

.

Система, в структуре которой есть последовательно присоединенное интегрирующее звено, называется астатической.

Если к трем предыдущим присоединить последовательно интегрирующее звено с передаточной функцией k 1/ T 1 p, получится передаточная функция

.

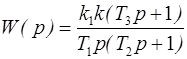В знаменателе появился множитель: комплексная переменная p. Последовательное присоединение еще одного интегрирующего звена даст множитель p 2. Говорят, в первом случае система обладает астатизмом первой степени, во втором – второй степени. В общем случае – астатизмом степени n.

Т.о. по тому, нет или есть в знаменателе передаточной функции множитель pn, системы делятся на два класса: статические и астатические.

В статической системе при постоянном входном воздействии выходная величина со временем становится постоянной, принимая значение, отличное от первоначального.

В астатической системе при постоянном входном воздействии выходная величина непрерывно изменяется.

 

 
Пример 4.10.

Наиболее простым астатическим звеном является интегрирующее, у которого

.

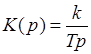Показать, что при постоянном входном воздействии выходная величина должна неограниченно возрастать.

Записываем операторное уравнение

,

вводим условие ступенчатого воздействия X (p) = 1 / p и получаем изображение переходной функции

.

В таблице изображений по Лапласу дроби 1 / p 2 соответствует оригинал t. Значит, переходной функцией будет

.

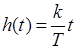Зависимость линейная, при t ® ¥ h (t) неограниченно возрастает.

 

 

 
Пример 4.11.

Можно ли получить астатическую систему, охватив интегрирующее звено жесткой обратной связью?

Записывая передаточные функции звеньев в виде

и

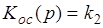
получаем передаточную функцию системы

.

Вводя новые постоянные: T = T 1 / k 1 k 2 и 1 / k 2 = k убеждаемся, что система имеет свойства инерционного звена:

.

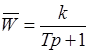То есть, система статическая. Однако, нетрудно убедиться, что при мягкой обратной связи система будет астатической.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)