 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Устойчивость системы по Гурвицу выясняется с помощью характеристического уравнения. Составляется специальный определитель – определитель Гурвица. Правило следующее
Намечают n строк и n столбцов (n – степень характеристического уравнения). В первый строке ставят все нечетные коэффициенты: a 1, a 3, a 5. По главной диагонали, начиная с коэффициента a 1, слева-вниз-направо располагают последовательно все остальные коэффициенты. Столбцы, начиная с главной диагонали, заполняются вверх по нарастающим индексам, вниз - по убывающим. Все коэффициенты с индексами ниже нуля и выше степени уравнения, заменяют нулями.
Определители Гурвица 5-го, 4-го, 3-го и 2-го порядков выглядят следующим образом.
n = 5 n = 4 n = 3 n = 2
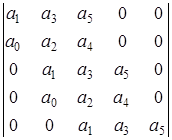
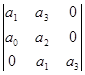
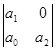
Для устойчивости системы необходимо, чтобы все коэффициенты характеристического уравнения и все определители были положительными.
Получим условия устойчивости для конкретных уравнений.
1. Характеристическое уравнение 2-й степени:
a0p2+a1p+a2 = 0.
Ему соответствует определитель Гурвица 2-го порядка:
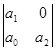= a 1 a 2- a 0 · 0 = a 1 a 2. D2 = a 1 a 2.
Условие устойчивости: a 0, a 1, a 2 > 0; D2 > 0, т.е. a 1 a 2 > 0.
2. Характеристическое уравнение 3-й степени:
a 0 p 3 + a 1 p 2 + a 2 p + a 3 = 0.
Ему соответствует определитель Гурвица 3-го порядка:
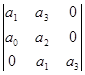= a 1(a 2 a 3 - a 10) - a 3(a 0 a 3 - 0 · 0) + 0(a 0 a 1 - a 2 · 0).
Δ3 = a 1 a 2 a 3 - a 0 a 23.
Условие устойчивости: a 0, a 1, a 2, a 3 > 0; Δ3 > 0, или, сокращая на a 3, a 1 a 2 – a 0 a 3 > 0.
3. Характеристическое уравнение 4-й степени:
a 0 p 4 + a 1 p 3 + a 2 p 2 + a 3 p + a 4 = 0.
Ему соответствует определитель Гурвица 4-го порядка:
= а 1 
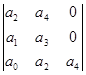- а 3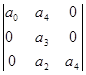 
+ 0 – 0.
Δ4 = a 1 a 2 a 3 a 4 – a 21 a 24 – a 0 a 23 a 4.
Условие устойчивости: a 0, a 1, a 2, a 3, a 4 > 0, Δ4 > 0, или сокращая на a 4, a 1 a 2 a 3 - a 21 a 4 - a 0 a 23 > 0.
4. Характеристическое уравнение 5-й степени:
a 0 p 5 + a1p 4 + a 2 p 3 + a 3 p 2 + a 4 p + a 5 = 0.
Опуская процедуру вычисления определителя, выпишем сразу условие устойчивости:
a 0, a 1, a 2, a 3, a 4, a 5 > 0,
(a 1 a 2 – a 0 a 3)(a 3 a 4 – a 2 a 5) – (a 1 a 4 – a 0 a 5)2 > 0.
Можно составлять определители Гурвица и для характеристических уравнений более высокой степени, получая соответствующие условия устойчивости. Однако, объем вычислений нарастает с увеличением степени характеристического уравнения, поэтому считается приемлемым пользоваться критерием Гурвица для характеристических уравнений степени не выше пятой.
Определитель Гурвица позволяет найти коэффициент усиления на границе устойчивости. Коэффициент усиления – это свободный член характеристического уравнения, его индекс равен степени уравнения. Границей устойчивости будет условие Δ = 0. Откуда и вычисляется коэффициент усиления.
Поиск по сайту: