Пример 2.5

Процесс в объекте описывается дифференциальным уравнением Найти переходную функцию.

Вводим условие единичного ступенчатого воздействия, полагая x = 1. Ищем решение дифференциального уравнения при нулевых начальных условиях. Решением будет переходная функция h (t), поэтому сразу можно y (t) заменить на h (t).

Общее решение неоднородного уравнения

есть сумма решений h ₁ + h ₂. Первое получают, решая однородное уравнение

.

Решением будет Второе решение h ₂ есть частное решение неоднородного уравнения, которое можно выбрать как h ₂ = k. Общим решением будет:

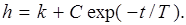
C учетом того, что h = 0 при t = 0, окончательное выражение для переходной функции получается в виде:

.

Найти переходную функцию для системы, описываемой дифференциальным уравнением

Запишем операторное уравнение

(5 p + 1) Y (p) = (3 p + 2) X (p)

в виде

Множитель при X (p) есть не что иное, как передаточная функция. X (p) – изображение произвольного воздействия. Воздействие в виде единичного ступенчатого скачка имеет изображение X (p) = 1/ p. Если в операторном уравнении заменить X (p) на 1/ p, то на Y (p) накладывается требование быть изображением переходной функции. Подчеркивая это, заменим Y (p) на H (p). Получаем операторное уравнение для переходной функции:

.

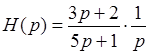Прежде чем воспользоваться таблицей изображений по Лапласу, представим правую часть уравнения в виде суммы:

.

В таблице находим оригиналы по их изображениям:

,

,

.

В нашем случае T = 5. Множители 3 и 2 сохраняют свое значение и место. Окончательно

,

или

h (t) = 2 – 1,4e ^{- t / 5}.

Литература

1. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.

2. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1989. – 304 с.

3. МакаровИ.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – М.: Машиностроение, 1977. – 464 с.

4. Гноенский Л.С., Каменский Г.С., Эльсгольц Л.Э. Математические основы теории управляемых систем. – М.: Наука, 1969.

Системы автоматического регулирования удобно представлять в виде соединения элементов, каждый из которых описывается алгебраическим или дифференциальным уравнением не выше второго порядка. При этом, одно и то же дифференциальное уравнение может описывать разные по своей физической природе элементы. Иными словами, у них одна математическая модель. Наиболее употребительные математические модели получили название типовых звеньев. Типовые звенья имеют одну входную и одну выходную величину.

Все конструктивное разнообразие САР можно представить небольшим числом типовых звеньев или их комбинаций.

Рассмотрим следующие типовые звенья.

Звенья, описываемые алгебраическими уравнениями:

- усилительное (пропорциональное),

- запаздывающее.

Звенья, описываемые дифференциальным уравнением первого порядка:

- инерционное,

- интегрирующее,

- дифференцирующее.

Звено, описываемое дифференциальным уравнением второго порядка. В зависимости от соотношения коэффициентов, оно может быть колебательным или апериодическим.

Характеристики типовых звеньев принято указывать для единичного ступенчатого входного воздействия.

Для полной характеристики типового звена следует указать его дифференциальное уравнение, операторное уравнение, передаточную функцию, комплексную, действительную, мнимую, амплитудную, фазовую, логарифмическую амплитудную, логарифмическую фазовую частотные характеристики и переходную функцию.

Поиск по сайту: