 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 5.8
Разомкнутая система имеет передаточную функцию
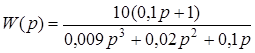 .
.
Выяснить устойчивость замкнутой системы.
Характеристическое уравнение замкнутой системы
0,009p3 + 0,02p2 +1,1p + 10 = 0.
Комплексный частотный полином, нечетный и четный полиномы:
D (jw) = - j 0,009 w 3 – j 1,1 w + 10 – 0,02 w 2,
V (w) = 1,1 w - 0,009 w 3,
U (w) = 10 – 0,02 w 2.
Частоты пересечения:
V (w) = 0, w 1 = 0, w 3 = 11,0.
U (w) = 0, w 2 = 22,4.
Требование чередования частот при последовательном возрастании не выполняется:
w 1 < w 2 > w 3.
Следовательно, система неустойчива.
Подтверждение этому получим, вычислив значения угла поворота вектора D (jw) при частотах пересечения с осями. Запишем тангенс аргумента:
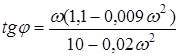 .
.
Вычисляем: ω 1 = 0, tg φ = 0, φ 1 = 0°.
ω 2 = 22,4, tg φ = -¥, φ 2 = -90°.
ω 3 = 11,0 tg φ = 0,00, φ 3 = 0°.
Угол φ не возрастает последовательно для каждой частоты пересечения. И не становится равным степени характеристического уравнения, умноженной на p/2.
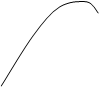
Как выглядит годограф Михайлова, показано на рис. 5.7.
 Таблица данных
Таблица данных
V
| ω | U | V |
| 9,5 | 4,4 | |
| 7,6 | ||
| 5,5 | -14 | |
| 22,4 | -76 |
 0 5 10 U
0 5 10 U
-40
-60
Рис. 5.7
Кривая не охватывает начала координат. Система неустойчивая.
Поиск по сайту: