 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 5.16
Дано характеристическое уравнение
p 3 + Mp 2 + Np + 1 = 0.
Произвести D - разбиение в плоскости параметров M и N.
Полагая p = jω, находим: - jω 3 – ω2M + jωN + 1 = 0.
Запишем для условий задачи систему уравнений (5.8). Если какой-то из полиномов Q 1, Q 2, R 1, R 2 окажется равным нулю, вместо него надо поставить ноль.
- ω 2 M + 0 N +1 = 0, - ω 2 M + 0 N = -1,
или
0 M + ωN - ω 3 = 0. 0 M + ωN = ω 3.
Определитель системы будет: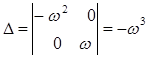 
.
Определители параметров:
. 
.
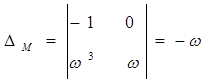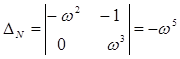Получаем: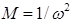 
, 
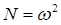. Функциональная зависимость между коэффициентами M и N представляет собой равнобочную гиперболу: MN = 1. График представлен на рис. 5.28.
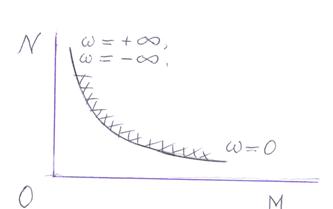
Рис. 5.28.
Верхняя ветвь гиперболы уходит в ¥ как для положительных, так и для отрицательных значений ω. Нижняя ветвь гиперболы уходит в ¥ при стремлении к нулю положительных и отрицательных значений ω. Учитывая эти обстоятельства, штриховка получается двойной: D < 0 при изменении ω от 0 до +∞ (штриховка справа) и D > 0 при изменении ω от -¥ до 0 (штриховка слева).
Поиск по сайту: