 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Ряд Тейлора
Обозначим через  сумму степенного ряда (1):
сумму степенного ряда (1):
 .
.
Из сказанного выше следует, что функция  является бесконечно дифференцируемой на интервале
является бесконечно дифференцируемой на интервале  , где
, где  -радиус сходимости ряда (1).
-радиус сходимости ряда (1).
Полагая  , получаем, что
, получаем, что  . Так как
. Так как
 ,
,
то, полагая  , получаем, что
, получаем, что  . Так как
. Так как
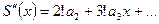 ,
,
то, полагая  , получаем, что
, получаем, что  . Рассуждая, таким образом, далее, приходим к тому, что
. Рассуждая, таким образом, далее, приходим к тому, что
 .
.
Таким образом, если какую-либо функцию в окрестности точки  можно разложить в степенной ряд (представить в виде суммы степенного ряда), то этот ряд единственный.
можно разложить в степенной ряд (представить в виде суммы степенного ряда), то этот ряд единственный.
Определение1. Пусть функция 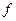 бесконечно дифференцируема на интервале
бесконечно дифференцируема на интервале  :
: 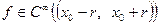 . Ряд
. Ряд
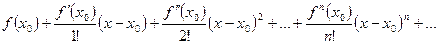
называется рядом Тейлора (при  рядом Маклорена) функции
рядом Маклорена) функции 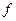 в окрестности точки
в окрестности точки  .
.
Поиск по сайту: