Критерий Коши сходимости несобственного интеграла первого рода. Достаточные признаки сходимости

Вопрос о сходимости несобственного интеграла первого рода эквивалентен вопросу о существовании предельного значения функци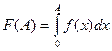и при 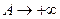. Как известно, для существования предельного значения функци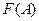и при 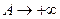необходимо и достаточно, чтобы она удовлетворяла следующему условию Коши; для любого ε>0 можно указать такое В>а, что для любых А₁ и А₂ превосходящих В, выполняется неравенство

.

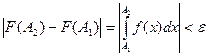
Таким образом, справедливо следующее утверждение.

Утверждение 1 (критерий Коши сходимости несобственного интеграла). Для сходимости несобственного интеграла (1.3) необходимо и достаточно, чтобы для любого ε>0 можно было указать такое В>а, что для любыхА₁ и А₂ превосходящих В,

.

Поскольку критерий Коши мало удобен для практических при­менений, целесообразно указать различные достаточные признаки сходимости несобственных интегралов.

В дальнейшем мы все время будем считать, что функция 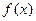задана на полупрямой 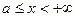и для любого 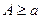существует обычный интеграл .

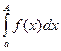Утверждение 2 (общий признак сравнения). Пусть на полупрямой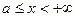

. (1.4)

Тогда из сходимости интеграла вытекает сходимость интеграла .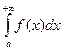

Утверждение 3 (частный признак сравнения). Пусть на полупрямой функция 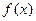удовлетворяет соотношению ; где с и λ – постоянные, λ>1. Тогда интеграл 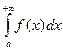сходится. Если же существует такая постоянная с>0, что на полупрямой справедливо соотношение в котором , то интеграл 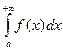расходится.

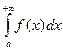Следствие (частный признак сравнения в предельной форме). Если при λ> 1 существует конечный предел , тоинтеграл сходится. Если при существует положительный предел 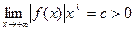, то интеграл 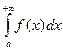расходится.

Поиск по сайту: