Критерий Коши сходимости ряда

Критерий Коши для сходимости последовательностей может быть легко перефразирован для рядов.

Действительно, как известно (см. п. 3.3), для того чтобы последовательность 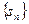была сходящейся, необходимо и достаточно, чтобы для любого 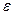>0 существовал такой номер , что для любых номеров и любых целых выполнялось неравенство

.

Для удобства использования этого критерия в случае рядов мы пишем здесь разность 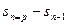вместо разности , которую писали раньше в п. 3.3. это, конечно, не влияет на суть дела. При этом, поскольку сумма не определена, мы всегда будем считать, по определению, =0.

Если теперь последовательность 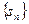является последовательностью частичных сумм ряда (35.1), то

,

и сформулированный критерий в этих обозначениях принимает следующий вид.

Теорема 4 (критерий Коши). Для того чтобы ряд 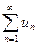сходился, необходимо и достаточно, чтобы для любого существовал такой номер , что при любом и любом целом выполнялось неравенство

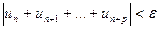(3.1)

Теорема 5 (необходимое условие сходимости ряда). Если ряд 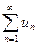сходится, то

. (3.2)

Действительно, в этом случае неравенство (3.1) выполняется для любого и, в частности, для р=0. поэтому для всех имеем

,

а это в силу произвольности и означает, что .

Теорема 5 доказана.

Кратко свойство (3.2) выражают, говоря, что «общий член ряда стремится к нулю».

Литература: 1, с.7-12; 7, с.257-260; 10,с. 501-507

Контрольные вопросы:

1. Сформулируйте определение числового ряда?

2. Что называют общим членом числового ряда?

3. Какую сумму называют n-ой частичной суммой ряда?

4. Какой ряд называют гармоническим?

5. Какой ряд называют рядом геометрической прогрессии?

6. Какой ряд называют сходящимся?

7. Какой ряд называют расходящимся?

8. Сформулируйте свойства сходящихся рядов.

9. Сформулируйте и докажите критерий Коши сходимости ряда.

10. Сформулируйте и докажите необходимое условие сходимости ряда.

Поиск по сайту: