О перестановке членов условно сходящегося рядов

Одним из важнейших свойств суммы конечного числа вещественных слагаемых является переместительное свойство. Естественно, возникает вопрос, остается ли справедливым это свойство для суммы сходящегося ряда, т.е. может ли измениться сумма сходящегося ряда от перестановки членов этого ряда. В этом пункте мы выясним этот вопрос в отношении условно сходящегося ряда. Начнем рассмотрение с изучения некоторой конкретной перестановки членов ряда

(3.1)

Ряд (3.1) сходится условно и имеет сумму . Переставим теперь члены ряда (3.1) так, чтобы после одного положительного члена стояли два отрицательных члена. В результате такой перестановки членов получим ряд

(3.2)

Докажем, что ряд (3.2), полученный в результате указанной перестановки членов ряда (3.1), сходится и имеет сумму, вдвое меньшую, чем ряд (3.1). Будем обозначать -е частичные суммы рядов (3.1) и (3.2) символами и 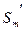соответственно. Можем записать:

.

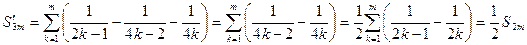Итак,

(3.3)

Далее, очевидно, что

(3.4)

(3.5)

Поскольку 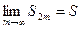, в пределе при из формул (3.8), (3.4) и (3.5) получим

, , .

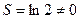Таким образом, ряд (3.2) сходится и имеет сумму, равную . Так как , то 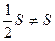. Следовательно, в результате указанной выше перестановки членов сумма условно сходящегося ряда (3.1) изменилась. Рассмотренный нами пример показывает, что условно сходящийся ряд не обладает переместительным свойством. Полную ясность в вопрос о влиянии перестановок членов на сумму условно сходящегося ряда вносит следующее замечательное утверждение, принадлежащее Риману.

Теорема 3 (Римана). Если ряд сходится условно, то, каково бы ни было наперед взятое число L, можно так переставить члены этого ряда, чтобы преобразованный ряд сходился к числу L.

З а м е ч а н и е. Аналогично можно было бы доказать, что если ряд сходится условно, то его члены можно переставить так, что последовательность частичных сумм преобразованного ряда не обладает переместительным свойством

Поиск по сайту: