Радиус сходимости и круг сходимости степенного ряда

Определение 1.1. Функциональные ряды вида

, (1.1)

где и - заданные комплексные числа, а - комплексное переменное, называются степенными рядами. Числа

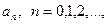
называются коэффициентами степенного ряда (1.1).

Если в ряде (1.1) сделать замену переменного, положив

,

то получим ряд

, (1.2)

Очевидно, что исследование сходимости ряда (1.1) эквивалентно исследованию сходимости ряда (1.2), поэтому в дальнейшем будем рассматривать ряды вида (1.2), употребляя, правда, как правило, для обозначения переменной букву , а не .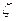

Теорема 1 (Абель). Если степенной ряд

, (1.3)

сходится при 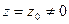, то он сходится и притом абсолютно при любом , у которого .

Следствие. Если степенной ряд (1.3) расходится при , то он расходится и при всяком , у которого .

Определение 1.2. Величина ( - число или символ ) такая, что при всех , у которых , ряд (1.3) сходится, а при всех , у которых , ряд (1.3) расходится, называется радиусом сходимости степенного ряда (1.3).

Множество точек , у которых , называется кругом сходимости ряда (1.3).

Теорема 2. У всякого степенного ряда (1.3) существует радиус сходимости . В круге сходимости, т.е. при любом , у которого , ряд (1.3) сходится абсолютно. На любом круге , где фиксировано и , ряд (1.3) сходится равномерно.

Теорема 3 (Абель). Если степенной ряд (1.3) сходится при , то он сходится равномерно на отрезке .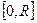

Следствие. Если степенной ряд (1.3) сходится при , то его сумма непрерывна на отрезке 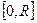. Это утверждение обычно называется второй теоремой Абеля о степенных рядах.

Теорема 4. Пусть - радиус сходимости степенного ряда

, (1.3)

тогда

, (1.4)

Формула (1.4) называется формулой Коши–Адамара.

Поиск по сайту: