 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метацентры и метацентрические радиусы
|
Читайте также: |
Предположим, что судно из исходного положения без крена и дифферента совершает поперечные или продольные равнообъемные наклонения. При этом плоскостью продольных наклонений будет вертикальная плоскость, которая совпадает с ДП, а плоскость поперечных наклонений – вертикальная плоскость, которая совпадает с плоскостью шпангоута, проходящего через ЦВ.
5.3.1. Поперечные наклонения. В прямом положении судна ЦВ находится в ДП (точка С) и линия действия силы плавучести γV также лежит в ДП (рис. 34). При поперечном наклонении судна на угол Θ изменяется форма погруженного объема, ЦВ перемещается в сторону наклонения из точки С в точку СΘ и линия действия силы плавучести будет наклонена к ДП под углом Θ.
Точка пересечения линий действия силы плавучести при бесконечно малом поперечном равнообъемном наклонении судна называется поперечным метацентром (точка m на рис.34). Радиус кривизны траектории ЦВ r (возвышение поперечного метацентра над ЦВ) называется поперечным метацентрическим радиусом.
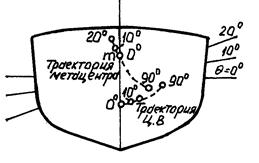
В общем случае траектория ЦВ является сложной пространственной кривой и каждому углу наклонения соответствует свое положение метацентра (рис.35). Однако для малых равнообъемных наклонений с известным приближением можно принять, что траектория
ЦВ лежит в плоскости наклонения и является дугой окружности с центром в точке m. Таким образом, можно считать, что в процессе малого поперечного равнообъемного наклонения судна из прямого положения поперечный метацентр лежит в ДП и своего положения не меняет (r = const).
 |
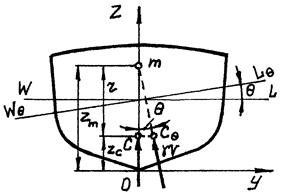 |
Рис.34. Перемещение ЦВ при Рис.35. Перемещение ЦВ при
малых наклонениях больших наклонениях
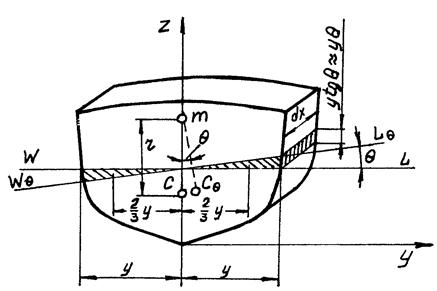 |
Выражение для поперечного метацентрического радиуса r получим из условия, что ось малого поперечного равнообъемного наклонения судна лежит в ДП и что при таком наклонении клиновидный объем v как бы переносится с борта, вышедшего из воды, на борт, вошедший в воду (рис.36).
Рис.36. К выводу выражения для поперечного метацентрического радиуса
Согласно известной теореме механики при перемещении тела, принадлежащей системе тел, центр тяжести всей системы перемешается в том же направлении параллельно перемещению тела, причем эти перемещения обратно пропорциональны силам тяжести тела и системы соответственно. Эту теорему можно распространить и на объемы однородных тел. Обозначим: С СΘ – перемещение ЦВ (геометрического центра объема V), b – перемещение геометрического центра клиновидного объема v. Тогда в соответствии с теоремой
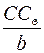 =
= 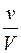 , откуда: С СΘ =
, откуда: С СΘ = 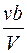 .
.
Для элемента длины судна dx, полагая, что клиновидный объем имеет в плоскости шпангоута форму треугольника, получим:
dv  dx
dx 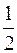 y tgΘ y,
y tgΘ y,
или при малом угле dv 
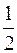 y2 Θ dx.
y2 Θ dx.
Если b 
 y, тогда: dv b =
y, тогда: dv b = 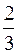 y3 Θ dx.
y3 Θ dx.
Интегрируя, получим: v b = 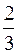 Θ
Θ 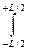 y3 dx,
y3 dx,
или: v b = ΘJx,
где Jx = 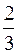
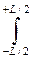 y
y  dx – момент инерции площади ватерлинии относительно продольной центральной оси.
dx – момент инерции площади ватерлинии относительно продольной центральной оси.
Тогда выражение для перемещения ЦВ будет иметь вид:
С СΘ = 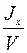 Θ.
Θ.
Как видно из рис. 36, при малом угле Θ
С СΘ  r Θ.
r Θ.
Сопоставляя выражения, найдем, что поперечный метацентрический радиус:
r = 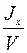 .
.
Аппликата поперечного метацентра:
zm = zc + r = zc + 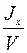 .
.
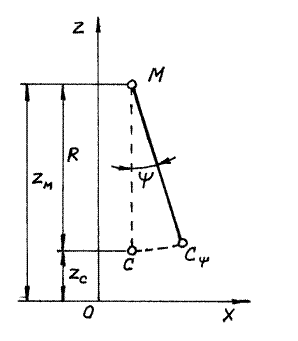 5.3.2. Продольные наклонения (рис.37). По аналогии с поперечными наклонениями точка пересечения линий действия силы плавучести при бесконечно малом продольном равнообъемном наклонении судна называется продольным метацентром (точка М на рис.37). Возвышение продольного метацентра над ЦВ называется продольным метацентрическим радиусом. Величина продольного радиуса определяется выражением:
5.3.2. Продольные наклонения (рис.37). По аналогии с поперечными наклонениями точка пересечения линий действия силы плавучести при бесконечно малом продольном равнообъемном наклонении судна называется продольным метацентром (точка М на рис.37). Возвышение продольного метацентра над ЦВ называется продольным метацентрическим радиусом. Величина продольного радиуса определяется выражением:
R = 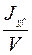 ,
,
где Jyf – момент инерции площади ватерлинии относительно поперечной центральной оси.
Рис.37.К выводу выражения
для продольного
метацентрического радиуса
Аппликата продольного метацентра:
zм= zc + R = zc + 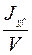 .
.
Так как площадь ватерлинии вытянута в продольном направлении, то Jyf намного превышает Jx и соответственно R значительно больше r. Величина R составляет 1 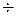 2 длины судна.
2 длины судна.
Метацентрические радиусы и аппликаты метацентров являются, как это будет ясно из последующего рассмотрения, важными характеристиками остойчивости судна. Значения их определяются при расчете элементов погруженного объема и для судна, плавающего без крена и дифферента, представляются кривыми Jx (d), Jyf (d), r(d), R(d) на чертеже кривых элементов теоретического чертежа (рис. 21).
Поиск по сайту: