 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Влияние приема малого груза на посадку и остойчивость судна
Изменение посадки судна при приеме груза рассматривалось в § 4.4. Определим изменение поперечной метацентрической высоты δh при приеме малого груза массой m (рис.49), центр тяжести которого располагается на одной вертикали с ЦТ площади ватерлинии в точке с аппликатой z.
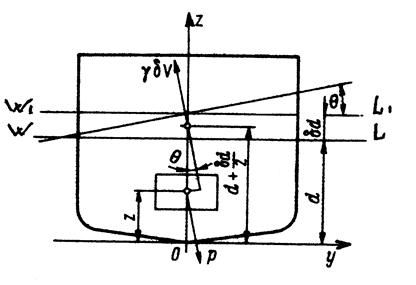 |
В результате увеличения осадки объемное водоизмещение судна увеличится на δV = m /ρ и возникнет дополнительная сила плавучести γ δV, приложенная в ЦТ слоя между ватерлиниями WL и W1L1.
Рис.49. Прием на судно малого груза
Считая судно прямобортным, аппликата ЦТ дополнительного объема плавучести будет равна d + δd /2, где приращение осадки определим по известным формулам δd = m/ ρS или δd = m / qсм.
При наклонении судна на угол Θ, сила веса груза р и равная ей сила плавучести γ δV составляют пару сил с плечом (d + δd /2 –z)sinΘ. Момент этой пары δmΘ = р (d + δd /2 – z) sin Θ увеличивает первоначальный восстанавливающий момент судна mΘ = γV h sin Θ, поэтому восстанавливающий момент после приема груза становится равным
mΘ1 = mΘ + δmΘ, или
(γV + γ δV)(h + δh) sin Θ = γV h sin Θ + γ δV(d + δd /2 – z) sin Θ,
перейдя к массовым значениям, получим
(Δ + m)(h + δh) sin Θ = Δ h sin Θ + m (d + δd /2 – z) sin Θ.
Из уравнения найдем приращение метацентрической высоты δh:

Для общего случая приема или снятия малого груза формула примет вид:
 или:
или:
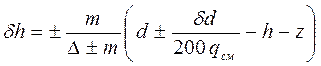 ,
,
где + (–)подставляется при приеме (снятии)груза.
Из формулы видно, что
δh < 0 при z > (d ± δd /2 – h) и
δh > 0 при z < (d ± δd /2 – h), а
δh = 0 при z = (d ± δd /2 – h).
Уравнение z = (d ± δd /2 – h) является уравнением нейтральной (предельной) плоскости.
Нейтральная плоскость, является плоскостью, прием на которую груза не изменяет остойчивость судна. Прием груза выше нейтральной плоскости уменьшает остойчивость судна, ниже нейтральной плоскости увеличивает ее.
Поиск по сайту: