Взаимодействие гребного винта и корпуса судна. Пропульсивный коэффициент

Винт и корпус судна находятся в сложном гидродинамическом взаимодействии. Сущность его заключается в следующем:

- на винт, работающий за корпусом, набегает поток воды, возмущенный движением корпуса, в результате чего гидродинамические характеристики винта изменяются по сравнению с их значениями в свободной воде;

- работающий винт изменяет величины давлений и касательных напряжений на поверхности кормовой оконечности корпуса, в результате чего изменяется сопротивление воды движению судна.

Следовательно, гидродинамические характеристики одного и того же гребного винта, работающего в свободной воде и за корпусом судна, будут различны, а сопротивление воды движению судна в присутствии работающего гребного винта будет отличаться от его буксировочного сопротивления.

11.7.1. Попутный поток. При движении судна часть окружающей его воды увлекается в направлении движения, образуя попутный поток (рис.115). Попутный поток за корпусом судна имеет в разных точках различное значение и направление, т.е. гребной винт работает в неравномерном поле скоростей, которое характеризуется осевыми, окружными и радиальными составляющими скорости попутного потока. При определении характеристик винта, как правило, учитывают только осевой попутный поток.

Из - за наличия попутного потока осевая скорость винта υ_p оказывается ниже скорости судна:

v_ω = v – υ_p,

где v_ω – осевая составляющая скорости попутного потока.

Отношение скорости попутного потока к скорости судна

v_ω / v = (v – υ_p)/v = 1– υ_p/v = ω

называют коэффициентом попутного потока.

С учетом коэффициента попутного потока, нетрудно получить следующее выражение для осевой скорости винта:

υ_p = (1 – ω)v.

В результате неравномерности потока по диску винта коэффициенты упора и момента винта за корпусом судна будут иными, чем в свободной воде. Указанное влияние учитывается:

- коэффициентом влияния неравномерности поля скоростей на упор

i₁ = ;

- коэффициентом влияния неравномерности поля скоростей на момент

i₂ = ;

- коэффициентом влияния неравномерности поля скоростей на КПД винта

i = = i₁/i₂.

В практических расчетах принимают i =1, основываясь на том, что коэффициенты неравномерности потока i₁ и i₂ изменяются в пределах 0,96 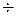1,02.

Рис.115. Попутный поток Рис.116. Формирование силы засасывания

за корпусом судна на корпусе судна: А - эпюра давления

при осутствии гребного винта; В- зона

давления при работающем винте

11.7.2. Засасывание. Работая за корпусом судна, гребной винт подсасывает воду и увеличивает скорость обтекания кормовой оконечности судна. При этом в соответствии с законом Бернулли понижается давление во всей зоне, охваченной подсасывающим действием винта, что увеличивает сопротивление формы (рис. 116). Кроме того, повышение скорости обтекания кормовой оконечности приводит к возрастанию сопротивления трения. Заштрихованная на рис. 116 область соответствует уменьшению давления в корме от работы гребного винта. В результате этих явлений появляется дополнительная сила ΔR, действующая на корпус и увеличивающая сопротивление воды движению судна. Эту силу принято называть силой засасывания. С учетом силы засасывания сопротивление движению судна

R' = R + ΔR,

где R - буксировочное сопротивление судна без гребного винта

Таким образом, часть упора гребного винта, именуемой полезной тягой Р_е, затрачивается на преодоление буксировочного сопротивления R, а остальная часть упора идет на преодоление силы засасывания, т.е.

Р = Р_е + ΔР.

Влияние засасывания принято учитывать с помощью коэффициента засасывания.

t = ΔР / Р = Р – Р_е = 1 – Р_е / Р.

С учетом коэффициента засасывания, упор винта Р

Р = Р_е /1 – t.

11.7.3. Значения коэффициентов взаимодействия. Коэффициенты ω и t весьма сложным образом зависят от формы корпуса судна, формы и расположения выступающих частей, от числа винтов, их геометрических характеристик и расположения по отношению к корпусу, от режима работы винтов, степени неравномерности поля скоростей в месте расположения винтов и других факторов.

Коэффициенты взаимодействия определяют экспериментальным путем или по приближенным формулам.

Для режимов работы винта, отличающихся от расчетного, коэффициент засасывания может быть определен по приближенной формуле Э.Э. Пампеля

t = ,

где λ_р - относительная поступь винта на рассматриваемом режиме; H/D - конструктивное шаговое отношение, t₀ - коэффициент засасывания на швартовом режиме (при λ_р = 0), который принимается равным (0,3 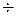0,6)ω или подсчитывается, если известны t и λ_р для расчетного режима, по формуле t₀ = t [1 – λ_р/(H/D)]; ω – коэффициент попутного потока для расчетного ходового режима.

Коэффициенты ω и t для расчетного ходового режима приближенно могут быть вычислены по формулам:

- для одновинтовых судов с обтекаемыми рулями

ω = 0,50δ – 0, 05; t = 0,80 ω,

- для двухвинтовых судов

ω = 0,55δ – 0,2; t = 0,25ω + 0,14 (с выкружками гребных валов),

t = 0,7ω + 0,06 (с кронштейнами гребных валов),

где δ - коэффициент общей полноты корпуса судна.

11.7.4. Пропульсивный коэффициент. Совершенство гидродинамического комплекса винт-корпус оценивается пропульсивным коэффициентом движителя η_д, который представляет собой отношение буксировочной мощности к валовой мощности затрачиваемой на вращение винта (§10.1.):

η_д = N_б / N_р = Rv/2πnM.

С учетом, что Р = Р_е /1 – t и υ_p = (1 – ω)v, получим

η_д = · (1 – t)/(1 – ω) = η_р η_к,

где η_р = Р υ_p/2πnМ - КПД гребного винта, работающего в свободной воде (§11.4.), а коэффициент η_к = (1 – t)/(1 – ω) - коэффициент влияния корпуса (§10.1.).

Поиск по сайту: