Кинематические характеристики гребного винта

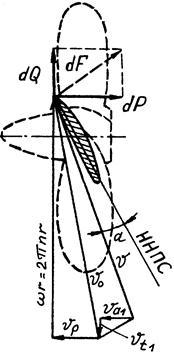
При изучении работы винта каждая лопасть рассматривается как совокупность отдельных элементов, обтекаемых независимо друг от друга плоским потоком (движение предполагается обращенным, т.е. элемент лопасти считается неподвижным, а поток воды - набегающим на него). Картина обтекания спрямленного элемента лопасти, заключенного между двумя соосными цилиндрическими поверхностями радиусов r и dr, приведена на рис.110. Поток набегает на рассматриваемый элемент лопасти с осевой скоростью υ_p и окружной скоростью ωr = 2πnr, где ω = 2πn - угловая скорость вращения, а

n - частота вращения винта. Работающий винт, как и всякий реактивный движитель, сообщает воде дополнительные (вызванные) скорости: он подсасывает воду к себе, а затем отбрасывает ее назад, создавая вызванную осевую скорость υ_а, и закручивает в направлении вращения, создавая вызванную окружную скорость υ_t. Вызванная скорость υ_а увеличивает осевую скорость, а вызванная скорость v_t уменьшает окружную скорость элемента лопасти относительно воды. В плоскости диска винта вызванные скорости составляют υ_а1 = υ_а/2 и υ_t1 = υ_t/2. Результирующая скорость потока, набегающего на элемент лопасти:

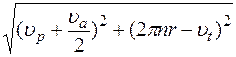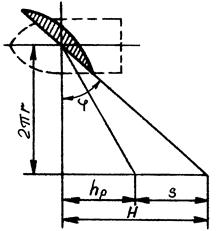Рис.110. Многоугольник скоростей Рис.111. Треугольник пути

и сил для сечения пройденного гребным винтом

элемента лопасти за один оборот

Окружные скорости для элементов лопасти, расположенные на разных радиусах, различны. Различна и результирующая скорость υ - она увеличивается от корневого сечения к краю лопасти.

Угол между направлением скорости υ и направлением нулевой подъемной силы (ННПС) называется углом атаки для элемента лопасти.

Если предположить, что винт движется в воде, как в гайке, т.е. без проскальзывания, то за один оборот он переместится в направлении оси вращения на величину геометрического шага Н. Фактически винт за один оборот перемещается в воде в осевом направлении на расстояние h_р, называемой поступью винта, причем h_р < H. При частоте вращения n винта его осевые (поступательные) скорости в твердой гайке и в жидкой среде соответственно равны Hn и υ_p = h_рn.

Отношение поступи винта к его диаметру называют относительной поступью винта:

λ_р = h_р/D = υ_p/nD.

Относительная поступь является универсальной кинематической характеристикой режима работы винта, поскольку изменение λ_р обусловливает изменение угла атаки набегающего на элемент лопасти потока как за счет изменения осевой скорости υ_p, так и окружной скорости 2πrn.

Разность H – h_р = S называется линейным скольжением винта. Из рис.111 видно, что линейное скольжение, как и поступь h_р, определяет угол атаки, а значит, и режим работы винта.

Важной кинематической характеристикой винта является относительное скольжение

s = S/H = (H – h_р)/ H = 1– h_р/ H = 1– υ_p/nH.

Между относительной поступью и относительным скольжением существует связь, которая определяется зависимостями

s = 1– 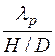; λ_р = 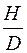(1– s).

Из зависимостей следует, что при s = 0: λ_р = ,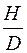

а при υ_p = 0: λ_р = 0; s = 1.

Поиск по сайту: