Свойства сходящихся рядов

Теорема 1. Пусть с – комплексное число. Если ряд

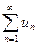
сходится, то ряд

,

называемый произведением данного ряда на число, также сходится и

. (2.1)

Эта теорема означает, что числовой множитель «можно выносить за скобку» и в случае бесконечного числа слагаемых, если они образуют сходящийся ряд. «Можно» в том смысле, что справедливо равенство (2.1).

Доказательство. Пусть

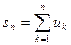и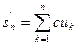

тогда, очевидно,

. (2.2)

По условию, существует, поэтому в силу (2.2) также существует и

,

это и есть равенство (2.1).

Теорема доказана.

Теорема 2. Пусть ряды

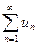и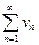

сходятся, тогда ряд

,

называемый суммой данных рядов, также сходится и

. (2.3)

Эта теорема означает, что сходящиеся ряды «можно складывать почленно» (n -й член с n -м), «можно» в том смысле, что справедливо равенство (2.3)

Доказательство. Пусть

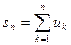, и ,

тогда

,

и так как и по условию, существуют, то также существует и

,

это и есть равенство (2.3).

Теорема доказана.

Поиск по сайту: