Сходимость функциональных последовательностей и рядов

Рассмотрим последовательности

(1.1)

и соответственно ряды

(1.2)

При каждом фиксированном значении аргумента эти последовательности и ряды, очевидно, представляют собой уже рассматривавшиеся числовые последовательности и ряды.

Пусть - некоторое множество элементов, в частности множество точек прямой, плоскости -мерного пространства или вообще элементов произвольной природы, и пусть (1.1) – последовательность функций, которые определены на множестве и значения которых являются, вообще говоря, комплексные числа.

Определение1.1. Последовательность (1.1) называется ограниченной на множестве , если существует такая постоянная , что для всех

и всех выполняются неравенства

(Иногда в этом случае последовательность (1.1) называется равномерно ограниченной.)

Определение1.2. Последовательность (1.1) называется монотонно убывающей (монотонно возрастающей) на множестве , если для всех

и всех выполняются неравенства

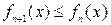
(соответственно, если для всех и всех выполняются неравенства

).

Это определение, очевидно, предполагает, что функции , принимают вещественные значения.

Определение1.3. Последовательность (1.1) называется сходящейся в точке , если числовая последовательность сходится.

Последовательность (1.1) называется сходящейся на множестве , если она сходится в каждой точке множества .

Если , , то говорят, что последовательность (1.1) сходится к функции , .

Аналогичное определение можно дать и для ряда (1.2).

Определение1.3’. Ряд (1.2) называетсясходящимся в точке , если сходится числовой ряд

.

Ряд (1.2) называется сходящимся на множестве , если он сходится в каждой точке этого множества.

Определение1.4. Ряд (1.2) называется абсолютно сходящимся на множестве , если на множестве сходится ряд

.

Подобно случаю числовых рядов, сумма

,

называется -й частичной суммой ряда (1.2); предел частичных сумм сходящегося на множестве ряда (1.2) называется его суммой :

.

Поиск по сайту: