Аддитивность интеграла Римана

Теорема 1. Пусть 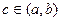. Тогда 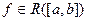тогда и только тогда, когда

одновременно и 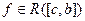. При этом

.

Пример 1. Рассмотрим функцию 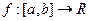, равную нулю всюду, за исключением точки .

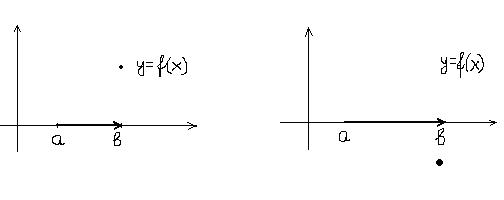
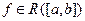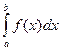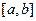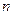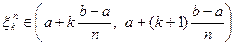Такая функция монотонна: в первом случае она неубывающая, во втором невозрастающая. Следовательно, . Найдем . Для этого разобьем отрезок на равных частей и в каждом из отрезков разбиения выберем точку . Тогда 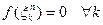, и тем самым

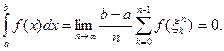
Точно также функция , равная нулю всюду, за исключением точки 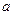, интегрируема и . Используя свойство аддитивности интеграла Римана, заключаем, что функция 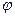, равная нулю всюду, за исключением конечного числа точек, интегрируема, и .

Теорема 2. Пусть 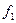и 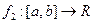отличаются лишь в конечном числе точек. Тогда 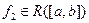и в том случае, когда они интегрируемы, интегралы их равны:

.

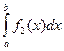Следствие 1. Если изменить значения функции 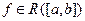в конечном числе точек, то полученная функция будет интегрируемой, а интеграл ее совпадет с интегралом функции .

Пример 2.

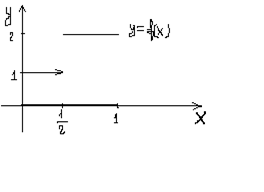Пусть .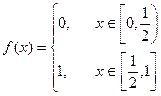

Найти .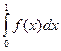

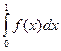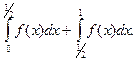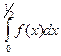Решение. = На отрезке функция постоянна и равна 2. Поэтому Для вычисления переопределим функцию в точке 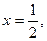положив 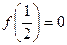. Полученная функция 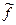тождественно равна нулю. Поэтому Следовательно,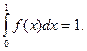

Поиск по сайту: