 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интегрирование выражений, содержащих тригонометрические функции
Символом  здесь и далее будем обозначать функцию, представляющую собой отношение двух многочленов переменных
здесь и далее будем обозначать функцию, представляющую собой отношение двух многочленов переменных  и
и  . Такая функция называется рациональной функцией двух переменных
. Такая функция называется рациональной функцией двух переменных  и
и  .
.
Аналогичным образом определяется рациональная функция трех переменных  , четырех и т.д.
, четырех и т.д.
Для вычисления интегралов  применяют универсальную тригонометрическую подстановку
применяют универсальную тригонометрическую подстановку  Тогда
Тогда



так что  .
.
Эта подстановка приводит часто к сложным выкладкам. Для отдельных классов тригонометрических функций более удобны следующие приемы интегрирования:
1. если функция  нечетна относительно
нечетна относительно  , т.е.
, т.е.  , то применяется подстановка
, то применяется подстановка  ;
;
2. если функция  нечетна относительно
нечетна относительно 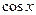 , т.е.
, т.е.  , то применяется подстановка
, то применяется подстановка  ;
;
3. если функция  нечетна относительно
нечетна относительно  и
и 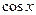 , т.е.
, т.е.  , то используется подстановка
, то используется подстановка  ;
;
4. если  и
и 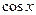 находятся в четных степенях, то применяют формулы понижения степени
находятся в четных степенях, то применяют формулы понижения степени 

Интегралы вида
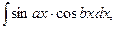


вычисляются с помощью известных формул тригонометрии преобразования произведения в сумму:
 ,
,
 ,
,
 .
.
Поиск по сайту: