Разложение правильной дроби на элементарные

Лемма 1. Пусть степень многочлена 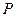меньше степени многочлена , который имеет вид

,

причём – многочлен и . Тогда правильная дробь единственным образом представима в виде

, (1)

где – многочлен с действительными коэффициентами. При этом вторая дробь в правой части равенства правильная.

Лемма 2. Пусть степень многочлена 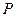меньше степени многочлена , который имеет вид

,

причём , и многочлен не делится на трёхчлен . Тогда рациональная дробь единственным образом представима в виде

, (2)

где – многочлен с действительными коэффициентами. При этом вторая дробь в правой части равенства правильная.

Леммы 1 и 2 позволяет утверждать, что любая правильная рациональная дробь допускает единственное разложение в сумму слагаемых, которые имеют вид

; (3)

, причём . (4)

Дроби этого вида называются элементарными.

Для фактического разложения правильной рациональной дроби используется так называемый метод неопределённых коэффициентов, состоящий в следующем. Сначала записывают знаменатель в виде

,

потом записывают разложение как сумму дробей вида (3) и (4) с неизвестными коэффициентами ( –в (3), и – в (4)). После приведения полученного равенства к общему знаменателю и его отбрасывания получают равенство двух многочленов. Приравнивая коэффициенты при одинаковых степенях, приходят к системе линейных уравнений для неизвестных коэффициентов. Таким образом, можно утверждать, что интегрирование любой рациональной функции сводиться к интегрированию многочлена и дробей вида (3) и (4).

Пример 1. Представить в виде суммы элементарных дробей функцию

.

Решение. Последовательно применяя Леммы 1 и 2, имеем:

,

отсюда

.

Приравнивая коэффициенты при одинаковых степенях , получаем систему уравнений:

Решая это систему, находим коэффициенты:

Поиск по сайту: